Traditional CV, mathematics more than deep learning

图像拼接问题

齐次坐标：

(这里的齐次坐标概念是在老师讲射影几何之前我自己对齐次坐标的理解)

欧氏空间中两条平行线不能相交，但它们在投影空间中是相交的，但我们用欧氏空间中的欧氏坐标没办法表达两条平行线在投影空间中相交的性质。怎么办？我们发明了齐次坐标。我认为，齐次坐标是用来表示欧氏空间中坐标的另一种方法，齐次坐标有以下几点好处：

齐次坐标兼容了欧氏坐标原有的性质
欧氏空间的欧氏坐标表示法不能用于证明两条平行线在投影空间相交，但齐次坐标能
齐次坐标能表达无穷远点的方向，例如(a,b,0)，而欧氏空间无穷远点只能是(inf,inf)。所以——齐次坐标是一个好工具。

每个欧氏坐标(x/w,y/w)有无穷多个齐次坐标(x,y,w)，但只有一个规范化齐次坐标(x/w,y/w,1)。不论是规范化还是非规范化的齐次坐标，都能唯一表示一个欧氏坐标。所以说，对于齐次坐标而言，x=kx,k!=0。

需要注意的是，欧氏空间中的点(不论是不是用齐次坐标表示)，分为两种：正常点；无穷远点。无穷远点没有规范化齐次坐标。

射影几何：

老师在讲完畸变镜头成像模型后开始讲这个的，我也不知道他讲射影几何是干什么用，我猜是为了引出齐次坐标吧，齐次坐标在处理成像原理、实现单目测量应该很有帮助。

首先要了解点积、叉积(即是求某个长度的法向量。有个行列式形式的公式比较好用，且容易用来推广运算混合积)、混合积(axb*c，代表求平行六面体体积)。

首先了解射影平面。

我们熟知的欧氏平面有两个限制，1.它没有无穷远点的概念；2.两个平行线不可能相交。

数学家们为了证明在某种条件，或者说，在某种概念下，两条平行线是有可能相交的，就引入了1.无穷远点，继而证明了2.两条平行线相交。这种被引入了无穷远点的欧氏平面即为射影平面。

那么，什么是无穷远点？我们首先要建立这样一个体系：假设欧氏平面pi0外有一点O，过O任一条直线与pi0上点一一对应，但实际上过O与欧氏平面平行的直线是不和pi0相交的，然后我们假设pi0上存在一组点，过O于pi0平行的直线与pi0在无穷远处相交于这组点，那么这组点就是无穷远点，过O任一条直线就与pi0上一点确实一一对应了。无穷远点怎么表示？本来，对于pi0上的普通点而言，每个点都对应于一条过O且与pi0相交的直线，若我们把O假设为离平面pi0距离为1，且O在3D空间中的坐标是(0,0,0)，其所在3D坐标系的x-y轴和pi0的x-y轴相同，pi0在O所在3D坐标系的z轴的(0,0,1)处。同时，过O的任一条直线由该直线方向所决定，即过O的直线方向对应于pi0上唯一一普通点——则，pi0上任一点可以表示为k(xi,yi,1)，(xi,yi)表示该点在在pi0上的坐标，1表示它在O所在3D坐标系下的纵坐标，k可以取任意非0值，它的值无关紧要，它不改变直线的方向。k(xi,yi,1)在表示过O直线的同时表示了pi0上的普通点，那么，k*(xi,yi,0)则表示过O且与pi0平行的直线，即对应了pi0上的无穷远点(再次强调有了无穷远点的欧氏平面就是射影平面了)。上述其实就是齐次坐标的由来，本身就是为了表示射影平面上引入的无穷远点k*(xi,yi,0)，从而推出平行线相交而生的。

由上面对射影平面上无穷远点的有趣定义和有趣表示，我们可以推导出，1.过O与pi0平行的直线与pi0上所有与该直线平行的直线交于同一个无穷远点(显而易见。假如相交于不同的无穷远点，则O上一直线对应于pi0上多于一个点，不一一对应，悖论。也符合两直线确定一点)；2.pi0上的两条平行直线交于无穷远点(由1推出，证明了两条平行线有可能相交的难题！)；3.一条pi0上的直线在无穷远处自己与自己交于一个无穷远点(无穷远点表示)，即射影平面上的直线实际上在射影平面上形成一个闭环；4.所有无穷远点构成一条无穷远直线(你可以这么理解，就是pi0上的直线与过O的平面一一对应，当过O平面是平行时，就对应了pi0上的无穷远直线)；5.若是齐次坐标x1和齐次坐标x2成比例，这它们表示的是同一个点。

下面我们将看到，射影平面上不仅点有齐次坐标，而且直线也有齐次坐标，两直线齐次坐标成比例同样说明这是同一条直线。在欧氏平面上，两点确定一条直线，但由于没有无穷远点，所以不能说两条直线确定一点，但在射影平面上，两条直线确实确定一点。

但首先我们来分析射影平面上，由两点确定一条直线，如何推导出该条直线的方程，进而得出表示直线的齐次坐标。假设有x点和x’点，如图

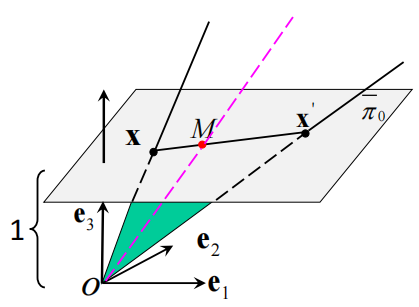
射影几何_1

则它们确定的直线xx’上的点m在Oe坐标系下所对应的直线Om必然跟Ox和Ox’在同一平面中，于是我们对这3条直线的方向向量做混合积的话，得到的结果应该是0，而方向向量可以直接射影平面pi0上的齐次坐标来表示，于是有式子 $\begin{bmatrix} x & y & z \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ \end{bmatrix} = 0$ (这也隐含了定理：射影平面上3点共线的充要条件是它们齐次坐标组成的3阶行列式为0)，展开得到直线xx’上点齐次坐标方程：ax+by+cz=0，我们把(a,b,c)即可看做直线xx’的齐次坐标，且根据混合机和叉乘的计算公式，我们可以看出，直线xx’齐次坐标就等于点x和点x’齐次坐标的叉乘。我们容易验证，若是两个直线的齐次坐标成比例，则两条直线是同一条直线，不信你把它们齐次坐标做个叉乘看看是不是0。而无穷远直线的齐次坐标也是同样的道理，你任取两个无穷远点做叉乘即可，要注意的是射影平面上的无穷远直线只有一个。 \[ \displaylines{ I_{\infty} = P_{\infty 1} \times P_{\infty 2} = (x_{1}, y_{1}, 0) \times (x_{2}, y_{2}, 0) = \begin{pmatrix} 0, &0, &\begin{bmatrix} x_1 & y_1 \\ x_{2} & y_{2} \end{bmatrix} \end{pmatrix} } \] 同样的，射影平面上两直线确定一点，点的坐标也是两条直线的叉乘。不难看出，射影平面上点和直线二位一体，完全绝对确实具有对偶性，例如“射影平面上3点/直线在同一直线/点上的充要条件是它们的齐次坐标组成的3阶行列式为0”。

自由度：

完全描述一个系统状态所需要的标量数。

图片拼接：

两张图片能拼接起来需要满足的前提条件：两张图片分别来自同一物理面的不同投影面。我们知道物理面和投影面之间的投影满足“射影定律”。

步骤：

标注两张图片的关键点。
给每个关键点打上描述子(向量)。
根据描述子匹配起两张图片的关键点。
列出两张图片的关键点所分属坐标系下的坐标(欧氏坐标即可)的线性变换方程组x’=Hx，并解出H。
应用H，将被拼接图片上的所有点都转换到拼接图片上去。

要走通以上5步，我们必须学习：线性几何变换、特征点检测与匹配

线性函数和仿射函数的区别：

线性函数的定义是：f(ax+by)=af(x)+bf(y)。所以y=Ax为线性函数，y=Ax+b仅为仿射函数，这是定义上的东西。

线性几何变换：

我们为什么要学线性几何变换？因为在图像拼接问题中，两张图像要能拼接在一起的前提之一是两张图片的像素点的坐标关系可以通过统一的线性几何变换H来表达，其中H是表达坐标变换的矩阵。若是不能用线性几何变换来描述两张图片像素点间的变换关系，则图像拼接的第4、5步将无法走动。

其实就是线性变换，我想，只不过是CV在研究几何学时的变换，所以是线性“几何”变换。

一个图像中的像素点发生了线性几何变换，即新图像上的像素点坐标较就图像像素点坐标发生了线性几何变换，在实际应用中原因往往是相机拍摄视角发生了变化。

线性几何变换的表达通式为T(x)=Hx，其中H非奇异，也就是说将x变换为T(x)后还能变换回来。
CV中研究的线性几何变换变换有5种，这5种并不是并列的关系，而是逐层宽泛、递进的关系，后者是前者的特例。在列举这5种线性几何变换之前，先理清几个概念：1.“保持角度”指的是圆/正方形不会变换成圆/平行四边形；2.“保持方向”指的是变换后的图像不会是原来的镜像；3.旋转统一指逆时针旋转；4.以下坐标都是规范化齐次坐标。这5种有线性几何变换有：

旋转变换/特殊正交变换：旋转；只考虑正常点；保持角度；保持方向；形式为 $H_{3 \times 3} = \begin{bmatrix} R_{2 \times 2} & 0_{2 \times 1} \\ 0_{1 \times 2} & 1 \end{bmatrix}$ ，要求R正交且det=1，R有通式 $R_{2 \times 2} = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$ ；自由度为1；长度不变。
(特殊)欧氏变换：旋转+平移(数学上还有一个反射，CV里准确来说该叫特殊欧氏变换)；只考虑正常点；保持角度；保持方向；形式为 $H_{3 \times 3} = \begin{bmatrix} R_{2 \times 2} & t_{2 \times 1} \\ 0_{1 \times 2} & 1 \end{bmatrix}$
，R正交且det=1；自由度为3；长度不变。
相似变换：旋转+平移+缩放；只考虑正常点；保持角度；保持方向；形式为 $H_{3 \times 3} = \begin{bmatrix} sR_{2 \times 2} & t_{2 \times 1} \\ 0_{1 \times 2} & 1 \end{bmatrix}$ ，s被称作缩放系数，R正交且det=1；自由度为4；相似比不变。
仿射变换：A作用于一点相当于先逆时针旋转$\phi$度$\rightarrow$沿X，Y轴做不同系数的缩放$\rightarrow$顺旋转$\phi$度$\rightarrow$逆时针旋转$\theta$度；只考虑正常点；不保持角度；当det(A)>0时保持方向；形式为 $H_{3 \times 3} = \begin{bmatrix} A_{2 \times 2} & t_{2 \times 1} \\ 0_{1 \times 2} & 1 \end{bmatrix}$ ，A非奇异；自由度为6，简单比(简单比的3点必须共线)不变。
射影变换(单应矩阵)：任意；考虑无穷远点；不保持角度；不保持方向；形式为cT(x)=Hx， $H = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}$ ，H非奇异(为什么有系数c？因为对于齐次坐标而言，Hx和kHx,k!=0是同一个欧氏坐标，这也是射影变换自由度为8而非9的原因)；自由度为8(你可以理解由于齐次坐标Hx=kHx,k!=0，H最后一行可以被简化为$\lbrack h_{31}/h_{31},h_{32}/h_{32},1\rbrack$，同样的道理，H=kH)；交比不变。

事实上，上述5大线性集合变换都是在对齐次坐标做操作，所以对于每个H而言，其实都有H=kH，只不过前4个我们把H中的h33元素钉死为1了，射影变换矩阵H我们刚好这里写的时候没有钉死为1。

上面说了CV中常见的几种线性几何变换，但由于我们在CV中研究的运动多是刚体的、保向的，也就是说，要保证运动的“刚体”，则线性几何变换变换不能有缩放(两点间距在变换前后都不变)；要保持运动的“保向”，则线性几何变换要保证方向——满足上述要求的只有旋转变换和欧氏变换，所以我们实际用的最多的是旋转变换和欧氏变换。

值得注意的是，任何一个正交矩阵可以代表一个旋转变换——当你的x不写成齐次坐标的时候，你的正交矩阵就不需要写成H的形式，直接取A。

上述5种线性几何变换变换分别构成群(一个定义了一种运算的集合，满足交结幺逆)，我们称之为变换群。而且由群的性质可推知：1.同类型的两种几何变换复合在一起，得到的仍然是这种类型的集合变换。好理解。我们给最常用的特殊正交群和特殊欧氏变换群起了名字，分别叫做SO(n)和SE(n)，n代表群的元素是n维的。

3维空间中的线性几何变换由此上类推。

特征点检测与匹配：

图像拼接的第4、5步我们已经通过学习线性几何变换掌握了，现在我们要打通1、2、3步，就要学习特征点检测与匹配。

具体是三步：1.特征点检测算法检测出特征点2.描述子构建算法打上描述子3.匹配两张图片的特征点。

其中，对于1中检测出来的特征点，我们希望它具备以下几点特性：

局部性/高判别性。特征点和周围其他的点应该很不相同，这便于特征点的定位。边缘上的特征点就不行，因为沿着边缘走，像素点基本相同。
稀疏性。特征点相对于图像全体像素而言应该是很少的。
对光照变化的稳定性。这就是面向特征点检测算法找特征点了，我们希望光照变化后算法还是能找到同样的特征点。
对几何变换的稳定性(包括尺度不变性、旋转不变性等)。同样是面向特征点检测算法找特征点，我们希望几何变换后算法还是能找到相同的特征点。

其中，对于2中的构建出的描述子，我们希望它具备以下几点特征：

高判别性/可分性。两个特征点的描述子差别极大。
对光照变化的稳定性/鲁棒性。当光照变化后，描述子不变。
对几何变换的稳定性/鲁棒性(包括尺度不变性、旋转不变性等)。相继拍摄视角发生了变化，描述子不变。

我们先来看第(1)步，特征点检测算法检测出特征点，核心在于该如何选取特征点？也就是说图像中怎样的像素点该被选取？有一种做法是选取哈里斯角点(简称角点，它其实不完全满足特征点的光照变化稳定性和几何变换稳定性，主要是几何变换稳定性中的尺度不变性，窗口大小被反映为特征尺度，所谓尺度不变性。但特征尺度的数值不一定等于窗口大小的数值。角点程度值和斑点响应值都是通过特征尺度内的像素计算出来的，但特征尺度不一定等于构建特征点描述子用的领域范围)。我们先预测有这样一种点，叫做角点，它具备稳定、稀疏、特殊的性质，可以作为图像的特征点，那么，如何判断一个点是不是角点？我们人为主观给地一个点开一个小小的“领域窗口”(窗口的大小是人为设定的超参数)，假如这个点沿着任何方向移动，它的领域窗口中的像素值都会发生很大变化，那么它就是角点。显然，在一片相同像素中的某一个点，或者图像直线边缘上的点都不是角点，而一个图形尖角上的一个点是角点——这是个典型的角点，也是“角点”名称的来源。

一个点是否为角点有一套量化的评判规则，评判指标为：使得该点领域窗口(窗口的大小是依经验选取的)在图像上移动至新位置后，新窗口的像素值和原窗口的像素值差值为1，此时的窗口位移量为$\Delta X$与$\Delta Y$，$\Delta X$与$Delta Y$值越相近，且越小，则该点越适合作为Harris角点。事实上$Delta X$和$Delta Y$的值相互制约，其值形成一个椭圆，我们希望这个椭圆是一个较小的正圆，而经过推导，该椭圆的长短轴大小仅依赖于该点在图像中位置附近的像素信息，且该位置附近像素信息可以被抽象成(邻域窗口二阶导矩阵)： $M = \left[ \begin{array}{cc} \sum\limits_{(x_i,y_i) \in W} \left( \frac{\partial f}{\partial x} \big|_{\substack{(x_i,y_i)}} \right)^2 & \sum\limits_{(x_i,y_i) \in W} \left(\frac{\partial f}{\partial x} \big|_{\substack{(x_i,y_i)}}\right) \left(\frac{\partial f}{\partial y} \big|_{\substack{(x_i,y_i)}} \right) \\ \sum\limits_{(x_i,y_i) \in W} \left(\frac{\partial f}{\partial x} \big|_{\substack{(x_i,y_i)}} \right) \left(\frac{\partial f}{\partial y} \big|_{\substack{(x_i,y_i)}} \right) & \sum\limits_{(x_i,y_i) \in W} \left( \frac{\partial f}{\partial y} \big|_{\substack{(x_i,y_i)}} \right)^2 \end{array} \right]$ 。f为以x,y为自变量，像素值为因变量的函数，xi和yi为该点领域窗口内的全部像素点。我们说，$Delta X$和$Delta Y$形成的椭圆的长短半轴依赖于M，我们可以从M中中提取出这样一个表达式(角点程度值)，来表示该点椭圆接近于小面积正圆的程度： $r(x)=det(M(x))-k(trace(M(x)))^2$ ，k值是依经验选取的，x表示一个像素点的坐标(x,y)，我们要让r(x)大于我们实现设定的阈值，则其被选为角点。那么，如何用程序计算图像中每个像素点的r(x)值？首先你要计算每个像素点的M，即1.先对所有像素点求一阶偏导(离散的数字图像的图像函数的偏导数是通过差分方法计算的)；2.再求二阶偏导；3.再做一次高斯模糊对每个像素点的领域窗口的所有像素点的二阶偏导数来一次求和，即得到了M(x)值；4.计算每个像素点的r(x)值，即得。

现在，Harris角点你已经找出来了，但遗憾的是，Harris角点满足稀疏性和局部性，但不满足对于整体光照变化以外的光照变化不变性，不满足对于旋转平移变换外的几何变换不变性。这里详细解释harris角点是如何不满足几何变换不变性中的“尺度不变性”的：根本原因在于该算法中使用的窗口大小W是人为预先设定的超参数，它不能适应不同图片的不同而相应变换大小，这也就导致了，一张图片上的A点通过窗口大小W计算出来是harris角点，但将该图片放大10倍，还是窗口大小为W，A就不是harris角点了——harris角点的判定严重依赖人为预先设定的邻域窗口大小，它的计算规则没有一种自动化的与图片尺度大小相适应的分析窗口大小设定机制。

我们先忘掉harris角点不能适应尺度不变性的缺点，先来看看其描述子的求法。

角点描述子求法常常是以角点x为中心开一个s*s的窗口W，然后基于W覆盖的图像区域构造特征描述子d。s的大小一般是用户预先设定的。

最naïve的描述子是块(block)描述子，它把W覆盖的区域拉成一个列向量并单位化。块描述子不仅不具备“尺度不变性”，还不具备“旋转不变性”。它很糟糕。

好了，我们暂定特征点是harris角点，描述子是block描述子。现在，你要开始图像拼接第3部：根据描述子匹配特征点。

先计算两张图像的各个描述子之间距离，方式有SAD(L1范数)，SSD(L2范数)、NNC(其实就是1-pearson)。然后开始匹配，假设两张图像中的特征点描述子集合为P,Q，两个匹配上的特征点的描述子分别是pi,qj，则pi和qj应该满足：

1. $dist(pi,qj) < threshold1$ ，大于阈值

2. $dist(pi,qj) < dist(pi, any\: qk\: in\: Q),dist(pi,qj)<dist(any\: pk\: in\: P,qj)$ 。双向奔赴

3. $dist(pi,qj)/second\_lowest\_dist(pi,qk) > threshold2$ ，不能模棱两可

现在貌似我们走到第3步了，但实际上或许从第一步选取特征点开始就是错的，我们要选取一个满足至少尺度不变性的特征点，选取一个至少满足尺度不变性和旋转不变性的描述子。

于是，我们引入了SIFT(scale-invariant featre transform尺度不变特征变换)特征点。特征点的选取有一个基本的超参数即邻域窗口大小/特征尺度，harris角点里的特征尺度是人为设定的，所以检测该角点的算法不能适应同一张图片放缩成不同大小，于是我们希望，一个特征点检测算法能够在不同size的同一张图片中自适应特征尺度，也就是说，特征点检测算法在检测一张图片的各个像素时，会自动开特征尺度，大size的同一个像素点特征尺度大，小size则特征尺度小——这就解决了特征点“尺度不变性”的需求。怎么实现这样的“自适应”？我们希望特征点检测算法在检测某一个位置(x,y)的像素时，会生成一个函数，函数的因变量是反映该点适合做特征点程度的响应值(类似于harris角点的角点程度值)，自变量是特征尺度的大小，该函数是先单增后单减，只有一个峰值，该峰值对应的特征尺度就被选为该点最终的特征尺度——于是，对于不同size图片中的同一个特征点，它的响应函数的特征尺度是自适应地不同的(但响应值应该是相同的，我想)。

SIFT特征点检测算法的响应函数是一个卷积，主要包含两部分，一部分是被指定位置的像素点的周边区域，一部分是卷积核，重要的也是卷积核的选取，选对了才能卷积出上述想要的响应函数。我们选出来的卷积核应该也是一个函数，核函数的自变量有3，x,y,特征尺度theta，x,y不重要，它是在卷积(x,y)位置像素的过程中才发挥作用，它们在响应函数图像中不会被体现出来，而theta，才是一个(x,y)像素点选取的不同特征尺度值，它是响应函数的自变量，重要。

我们最终选取出来的卷积核函数叫尺度归一化高斯函数的拉氏算子(scale-normalized Laplacian of Guassion，又称尺度归一化LoG)，高斯函数是： \[ g(x,y)=\frac{1}{2\pi\sigma ^2} exp\left( - \frac{x^2+y^2}{2\sigma^2} \right) \] 高斯函数的拉氏算子是： \[ \nabla^2 g = \frac{\partial^2 g}{\partial x^2} + \frac{\partial^2 g}{\partial y^2} = \frac{x^2+y^2-2\sigma^2}{2\pi\sigma^6} e^{-\frac{x^2+y^2}{2\sigma^2}} \] 尺度归一化的高斯函数的拉氏算子就是在前者乘上个sigma^2： \[ \sigma^2 \nabla^2 g = \frac{x^2+y^2-2\sigma^2}{2\pi\sigma^4} e^{-\frac{x^2+y^2}{2\sigma^2}} \] 即： $\sigma_{i}^{2} \nabla^2 g(\sigma_i)$

将尺度归一化LoG的theta固定住，你会发现它在x-y空间中像一个倒置的墨西哥草帽，草帽的积分为-1：

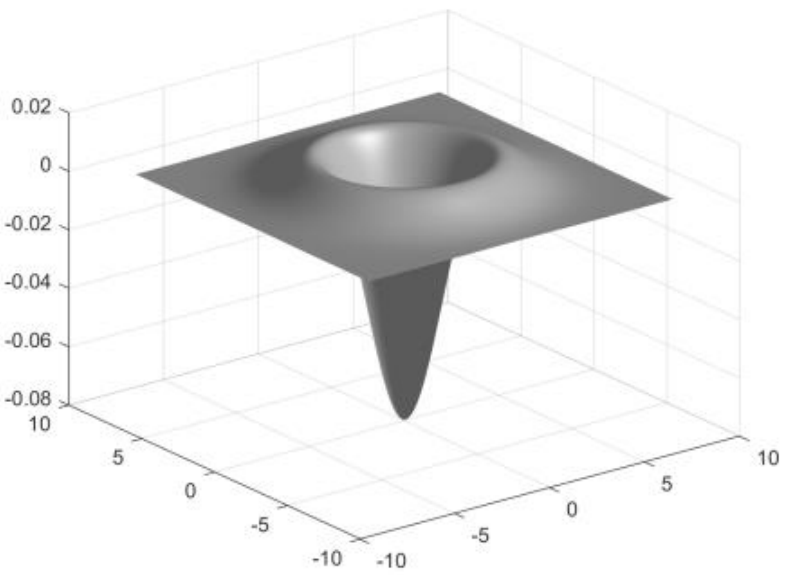
特征点检测与匹配_1

所以，用这个卷积核函数去对图像像素值做卷积，再选取峰值theta做特征尺度，你理想情况将得到一个圆斑，圆斑里面亮度很低，圆斑外面亮度很高，theta即为圆斑的半径。故而SIFT特征点又称作“斑点”blob。

Theta选出来的特征尺度天然能作为特征点描述子采样的的邻域窗口大小，于是特征点描述子的尺度不变性问题也解决了。

接下来，我们计算图像的响应值，3变量空间，结果如下：

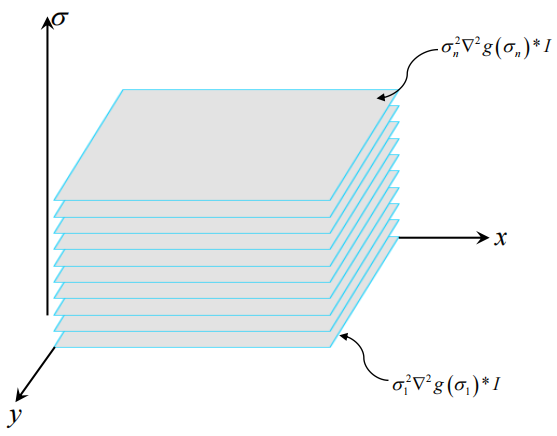
特征点检测与匹配_2

我们选取SIFT特征点的方法类似于从一堆角点程度值里选harris角点。

我所推测的简单的特征点检测算法流程是：

计算每个像素在一定范围theta内的响应值。有一个计算每个像素点尺度归一化LoG的trick：为了减小计算量，且保证LoG值计算的精度，可以选则在计算较大theta的LoG值时，将图像的分辨率调小，这对计算结果没有影响。
先选取每个像素的特征尺度大小：对于每个(xi,yi)的像素点而言，其在theta轴方向上只有一个theta最优解使得其响应值最大，取该响应值为该像素的最终响应值。
比较该点在3维变量空间上下左右前后的26个邻居的响应值，若是该点响应值比邻居都大，则其被选为候选特征点，特征尺度为theta。
接下来的过程张林没有详讲，我想应该是设置阈值从候选特征点中再抽取一批，再用nms吧……

具体特征点检测算法的流程其实比这个复杂得多，在实际应用中，甚至是用一个叫做DoG的东西去近似尺度归一化的LoG，这里只是说一个大概的思想。

严格来讲，SIFT并不是上述特征点的名称，上述特征点叫做斑点其实更合适(对应角点)，SIFT尺度不变性特征转换其实是整套检测斑点+构造其特征描述子的算法。下面将介绍这种算法构造特征点描述子的大致流程：

首先你前面检测出特征点了(解决了harris角点的尺度不变性)，也顺带检测出其特征尺度(解决了block描述子的尺度不变性)，于是将特征尺度也用作特征点描述子的邻域范围。
接下来你要确定邻域主方向，以便后面将两张图像的特征点描述子描述的特征对齐，同时，这也解决了block描述子的旋转不变性问题。确定主方向的方法是：计算特征点邻域范围(SIFT算法中不等于特征点尺度空间)内所有像素的梯度方向，然后做出0~2*pi的梯度方向直方图，挑选y值最大的角度作为邻域主方向。
构建特征点描述子。在特征点的邻域范围内划分出44共16个小区，每个小区再计算出一个长度为8的梯度方向直方图，这样你就得到了一个44*8=128的特征描述子，描述子还要做归一化以解决光照不变性问题。

上述所有SIFT算法步骤只是个大概，很多细节都没涉及，但是差不多是这个意思。反正，现在你已经解决了图像拼接的1,2步，满足了特征点的尺度不变性和旋转不变性(harris角点也满足旋转不变性)，满足了特征描述子的尺度不变性和旋转不变性和关照不变性，现在你可以顺理成章解决图像拼接第3步了。

求解线性变换方程组：

现在进入了图像拼接的第4步，求解线性变换方程组。

两张图像可拼接的前提条件是其上面所有的点都满足射影变换。射影变换(projective transformation)又称单应变换(homography transformation)，其严格定义难求得，我们说一个简单的最常用的情景：一般情况下，对同一个平面上的点拍照(假设镜头无畸变)得到的两张不同图片，都满足射影变换，那什么时候不满足呢？若是被拍照上的点不全在一个平面上，则两张照片不满足射影变换，例如，被拍照场景是一个透视场景，一栋楼在你面前，一栋楼在很远处，这样图像拼接出来多少看起来有点别扭。如图，c点是相机，矩形是照片：

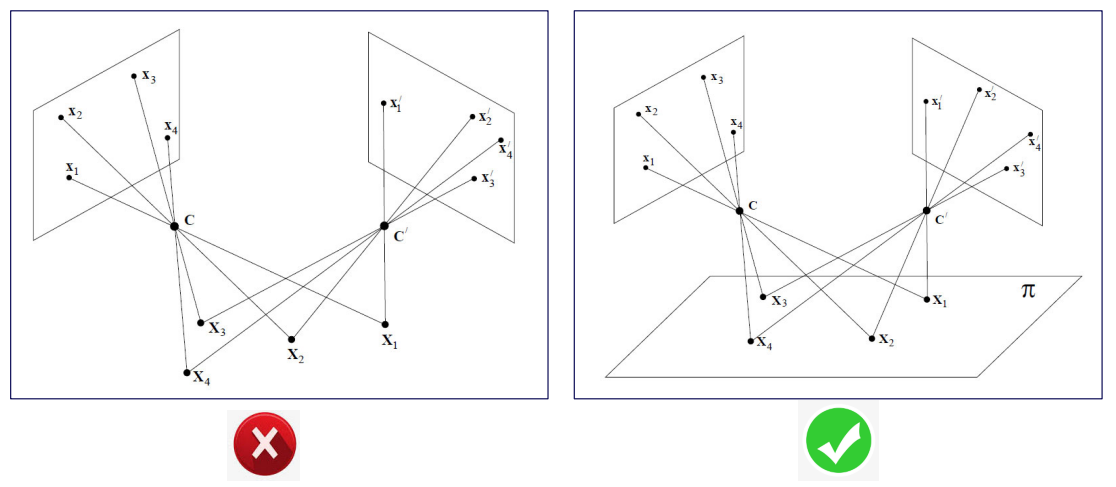
求解线性变换方程组_1

这种形如相机拍照的，最简单常见的满足射影变换关系的情景里：射影变换矩阵/单应矩阵是3*3的，它描述的是2D空间到2D空间间的射影变换。

这里的图像拼接问题，显然满足射影变换，于是我们能列出射影变换方程： $c \times y_i=H \times x_i$，这里的xi,yi都是齐次方程，对于每一个点i而言，c的取值都可以是任意的，也就是说下式都成立： \[ \displaylines{ c \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} } \] 这里的c无关紧要，因为反正该式子都可以化作： \[ \displaylines{ \frac{h_{11}u + h_{12}v + h_{13}}{h_{31}u + h_{32}v + h_{33}} = x \\ \frac{h_{21}u + h_{22}v + h_{23}}{h_{31}u + h_{32}v + h_{33}} = y } \] 然后化作 $A_i \times h=0$ 的形式： \[ \displaylines{ \begin{bmatrix} u & v & 1 & 0 & 0 & 0 & -ux & -vx & -x \\ 0 & 0 & 0 & u & v & 1 & -uy & -vy & -y \end{bmatrix} \begin{bmatrix}h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \end{bmatrix} =0 } \] 解 $A_{2n\times 9}\times h_{9*1}=0_{2n\times 1}$ 即可($A\times h=0,A\times x=y$这些形式的式子什么时候有解？注意复习线性代数)。

当然，由于有齐次坐标方程组中c值可以取任意的存在，所以H阵的h33能被化作1(射影变换自由度为8)，所以上面的方程组就可以化简为： \[ \displaylines{ \begin{bmatrix} u & v & 1 & 0 & 0 & 0 & -ux & -vx \\ 0 & 0 & 0 & u & v & 1 & -uy & -vy \end{bmatrix} \begin{bmatrix}h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \end{bmatrix} =\begin{bmatrix}x\\y\end{bmatrix} } \] 注意此时化出来等式右边就不是0向量了。解$A_{2n\times 8}\times h_{8\times 1}=b_{2n\times 1}$即可。

在解线性代数方程时常用到10个结论：

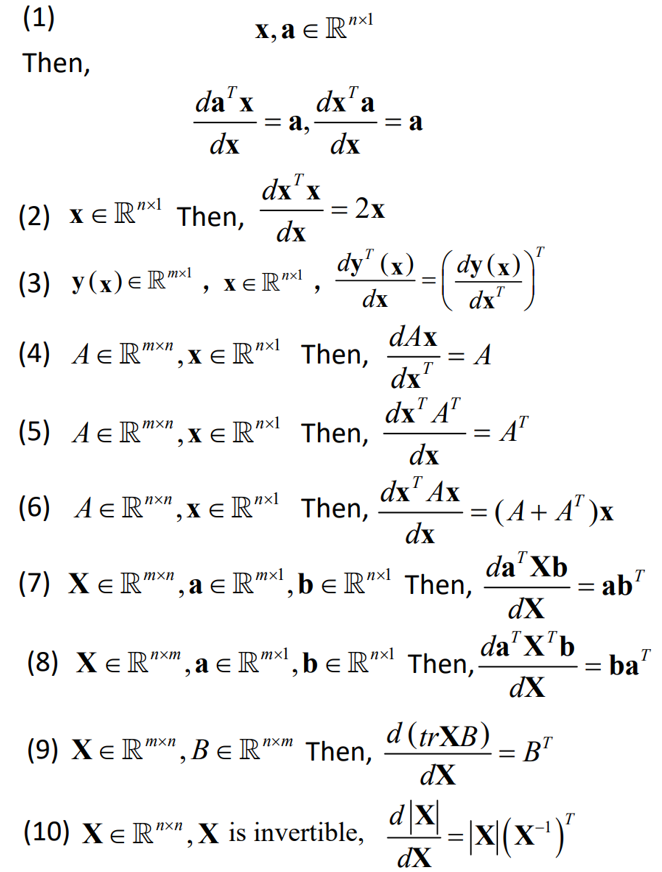
求解线性变换方程组_2

行向量不能对行向量求导，求导的结果的形状取决于微元的形状。标量对行向量求导得到行向量，列向量对行向量求导得到矩阵。

但要注意的是，上述两种形式的方程组都往往是不可解的，我们往往只能计算出一个解，使得$\Vert A_{2n\times 8}\times h_{8\times 1}-b_{2n\times 1} \Vert ^2$最小，这个时候就要对$\Vert A_{2n\times 8}\times h_{8\times 1}-b_{2n\times 1}\Vert ^2$求导数，取函数峰值。我们要解的往往最终是： \[ x^{*}= \mathop{\arg\min}\limits_{x} \textit{E}(x) = \mathop{\arg\min}\limits_{x} \Vert Ax - b \Vert_2^2 \] 要注意的是，当求$A_{2n\times 9}\times h_{9\times 1} = 0_{2n\times 1}$时(一般不这样做)，为了防止解出来的h=0，我们会人为加上一个条件$\Vert h \Vert=1$，于是上述方程就变成了一个带约束条件的求一个函数的极值点解，这个时候你要用到拉普拉斯乘子法：

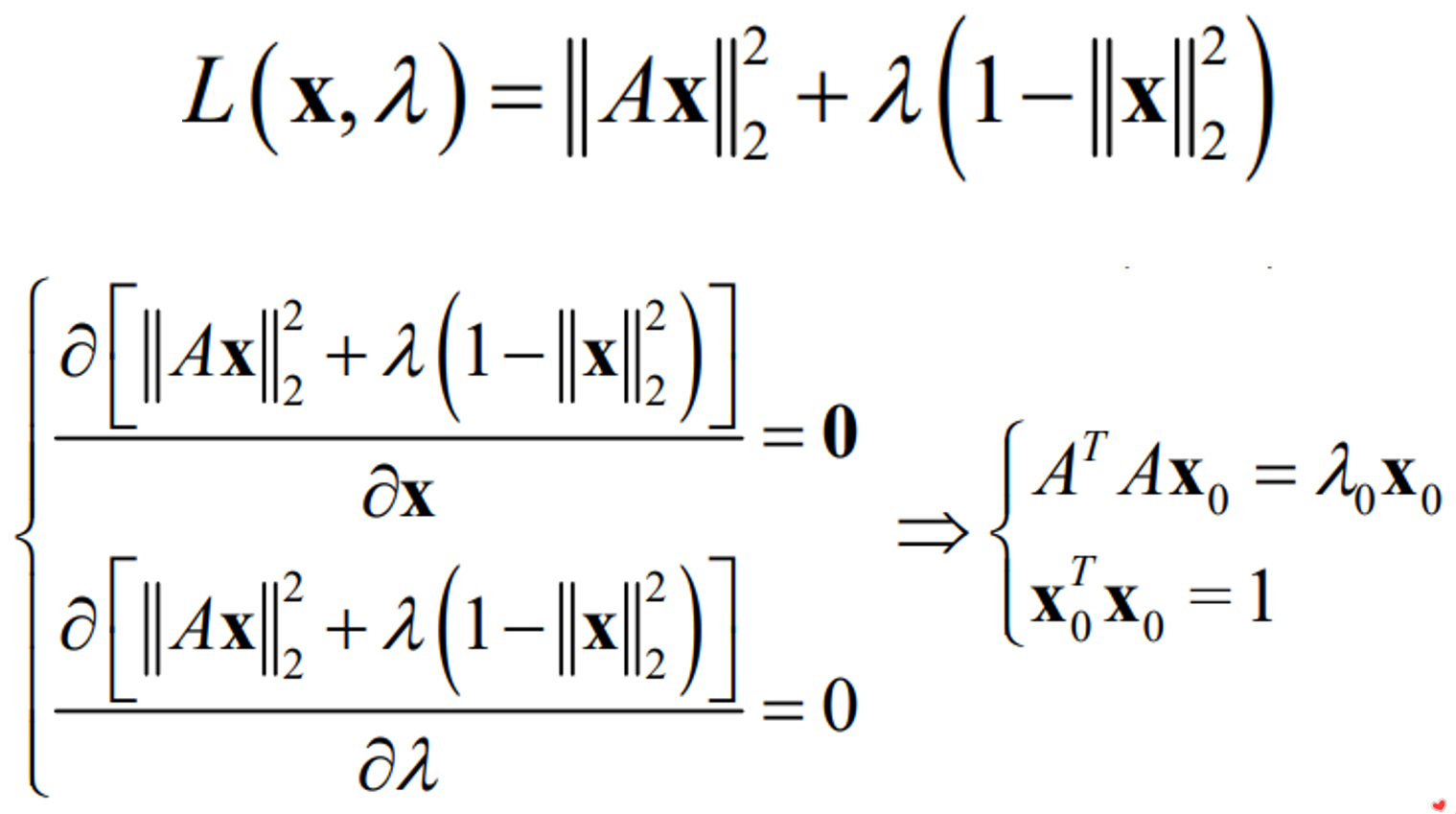
求解线性变换方程组_3

要注意到的是，不论是解$A_{2n\times 8}\times h_{8\times 1}=b_{2n\times 1}$还是解$A_{2n\times 9}\times h_{9\times 1}=0$，n都至少是4，因为当n刚好等于4时，h有一个线性无关的解，当n大于4时，解h就要用到线性最小二乘法了，这里不多讲，自己查书。为什么n一定要为4？正统地，是线性代数的知识；不正统地，h有8个自由度，A的每个行构成一个线性方程，消除一个自由度。

在求解线性变换方程组的时候，我们默认了通过描述子匹配两张图像的特征点的匹配是完全正确的，即没有两个特征点匹配错误的情况。但在现实中，是很有可能存在特征点匹配错误的情况的，匹配错误的特征点对(x,y)(u,v)叫做外点，正确的我们叫做内点，它会影响求出来的线性几何变换矩阵H的精度，为了排除外点对H的干扰，我们引入了随机抽样一致算法(RANSAC，Random Sample Consensus)。该算法的伪代码是：

求解线性变换方程组_4

你应该对这个简单的算法有一个基本的了解，我就不详细解释这个伪代码了，但我要告诉你的是，在图像拼接问题中，data表示的是所有在第3步描述子匹配过程中匹配上的特征点对，可以把(x,y)视作自变量，(u,v)视作因变量；n是你设置的超参数，表示每次随机采样时所需要的点对数，在这里，应该设置为4，因为上面已经说过，要准确地求解h，至少要有4个点对；k,t,d也是人为设定的阈值，要注意的是t表示误差，即是||H*(x,y,1)-(u,v,1)||，要注意d表示一致集中的内点的个数，要注意k作为最大迭代次数，指的是从头开始随机采样到最后计算出d值，整个过程要做多少遍，k的选取其实不完全是人为，它也有一套计算规则，我这里不详述。你最终得到的bestFit是你选定的使得d值取得最大时的一致集中的全部内点，把这些内点用于最后的计算，得到最终的H。

图像的插值：

到目前为止，你已经走通了图像拼接的前4步，就剩最后一步，如何把仿射变换矩阵H应用到两张图像中的全部点，拼接在一起呢？这一步要用到图像插值，图像插值的意思是根据周围整数坐标点的像素值估计出中间非整数坐标点的像素值，为什么我们会用到这个？因为：若是我们用传统的做法，对第一张图片上的像素点做H(x,y,1)计算出对应于第二张图像上的像素点坐标(u,v,1)，然后把(x,y,1)上的像素值直接赋值上去，会发现(u,v,1)是个非整数，你赋值赋给谁？所以我们反向思考，通过(u,x,1)H^-1计算出对应的(x,y,1)的非整数坐标点，然后根据(x,y,1)周围整数坐标点的值应用“图像插值”计算出对应的(x,y,1)即(u,v,1)的像素值即可。

图像插值的算法有很多中，用的最多的是双线性插值，很简单，你会。

现在我们进入下一个阶段：单目测量问题

单目测量问题：

前提假设：待测量目标位于一个物理平面上(此即保证了射影变换)，图像平面与该物理平面之间满足线性几何变换(通常是相似变换)。

于是，你要在单张图像上对目标大小和位置进行测量。这就是单目测量。

单目测量大致分为两个步骤：1.内参标定；2.外参标定。

内参标定是为了去畸变，由于相机成像过程往往不满足针孔相机成像模型，所以图像往往有镜头畸变，畸变的图像是不会和物理平面有相似变换的。所以我们要对图像去畸变，就要知道包括畸变系数在内的相机的所有内参数，相机内参数指的是在参数化相机成像模型中与相机自身性质有关的参数，其与相机所处外在空间无关。内参标定以去畸变的根本目标是为了满足单目测量的前提假设——图像与物理平面的相似变换。

外参标定就是为了确定去畸变后的相机成像平面与目标物体所处平面间的线性几何变换H。外参指离线外参数。得到了H后就可以根据图像对物理平面上的目标大小和位置进行测量了。

针孔相机成像模型：

在介绍内参标定和外参标定之前，我们先要弄懂相机的成像原理，现实世界中的相机往往不满足针孔相机成像原理，例如鱼眼相机(我们对其进行内参标定以去畸变)，在我们介绍这些复杂相机的成像原理之前，我们先介绍简单的针孔相机，以便你对什么是内参，什么是外参有一个直观上的认知。

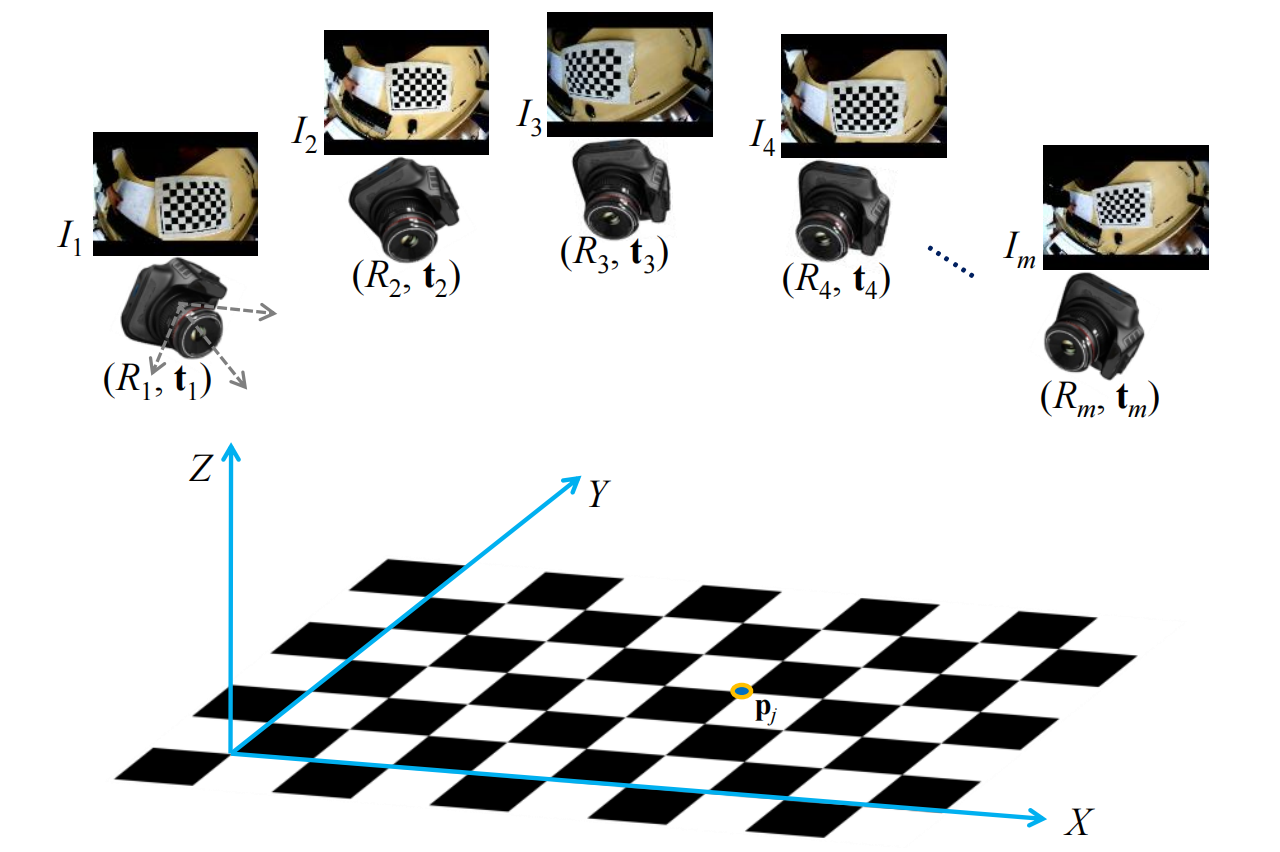
我们认识针孔相机成像原理的过程，即是推导物理世界中一点如何变换成图像平面上一个像素点坐标的过程，先来看一张示意图(注意这张示意图中，蓝色的x-y坐标轴，是世界坐标系，看上去它好像跟成像平面坐标系是重合的，实际上不是这样的。事实上，世界坐标系常由标定板确定)：

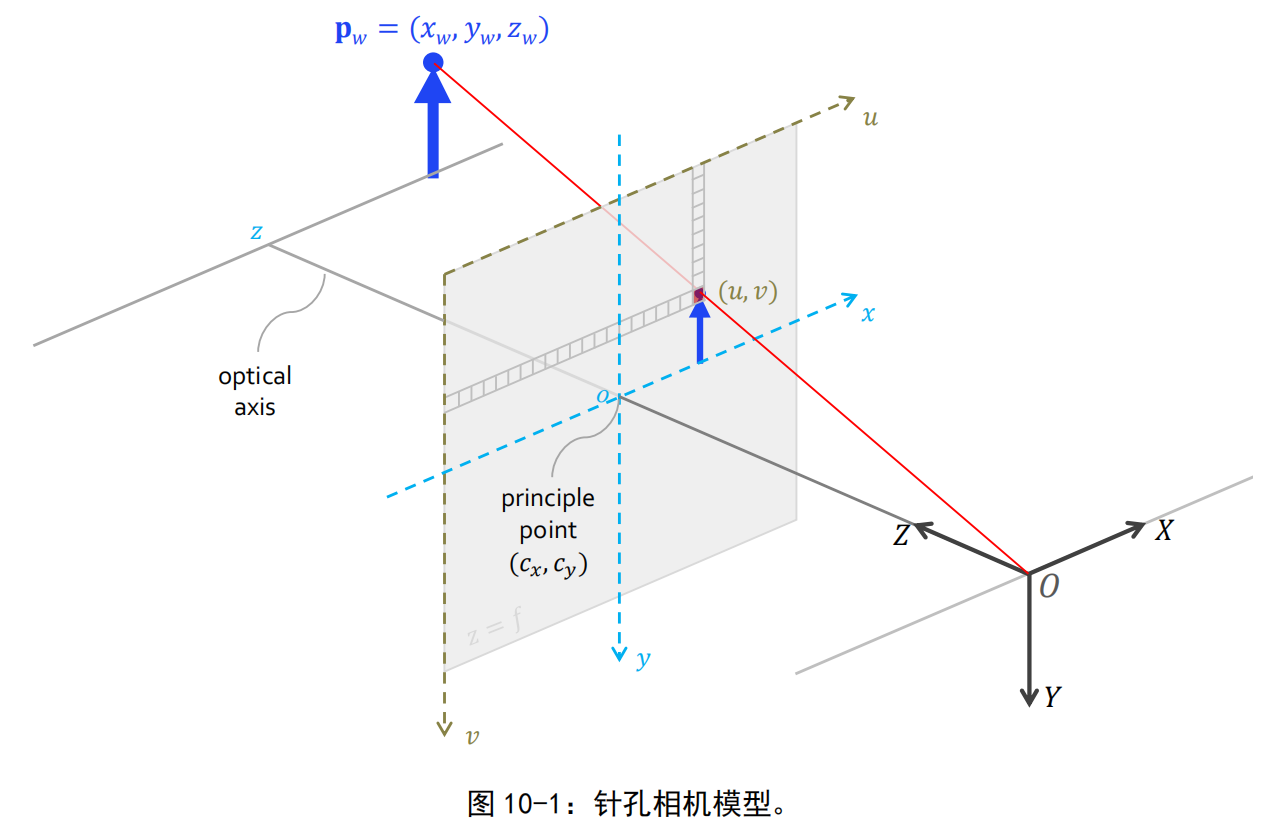
针孔成像模型_1

现在有3个坐标系，一个3D世界坐标系，原点及坐标轴方向未知；一个3D相机坐标系，原点是相机光芯；一个2D成像平面坐标系，原点是其中心(其上还有一个将坐标点像素化的像素坐标系)。我认为，转移3个坐标系中单位的度量是一样的，例如一个单位长度是1m。
世界坐标系中有个齐次坐标pw(Xw, Yw, Zw, 1)，先将它通过3D空间中的欧氏变换转移到相机坐标系中的pc(为了方便我们就选用非齐次)，欧氏变换分为两部分，一部分R33表示旋转且正交且det=1，一部分t31表示平移。于是我们可以根据世界坐标系中的齐次坐标得到相机坐标系中的pc：
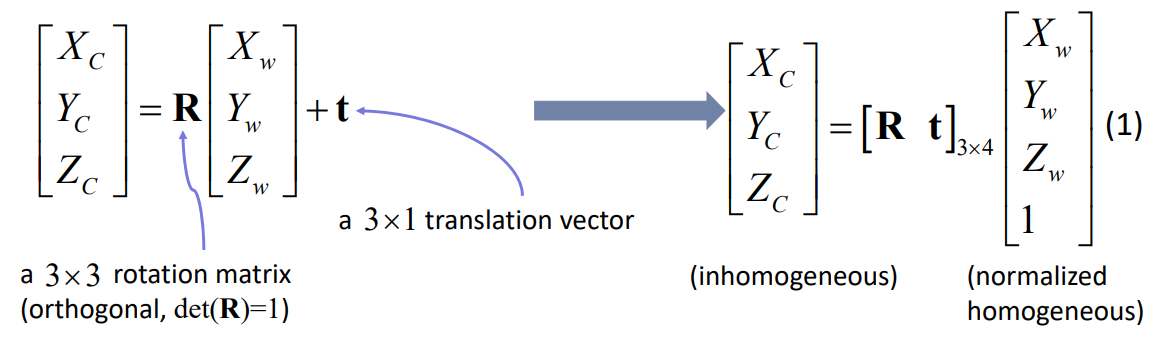
然后我们把3D相机坐标系中的pc(Xc, Yc, Zc)变换到2D成像平面坐标系中的(x, y)：

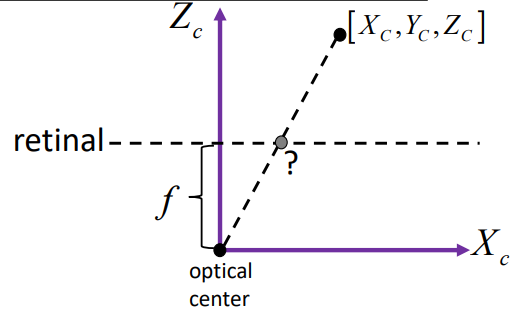
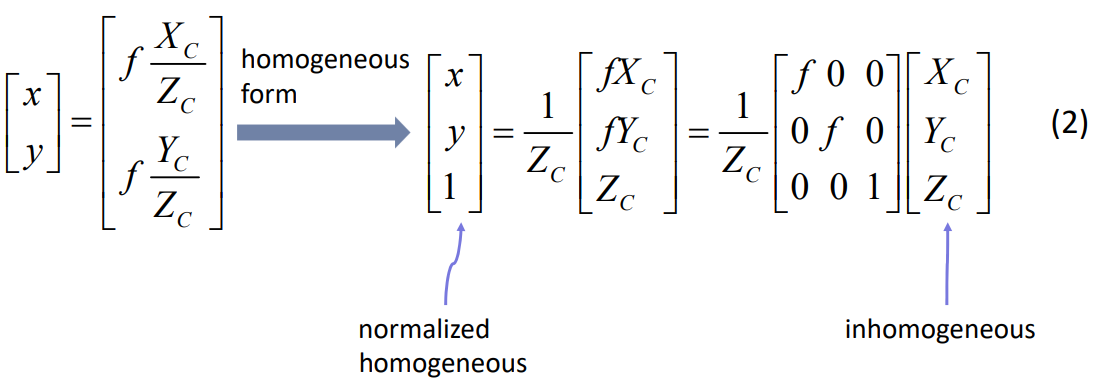
我们为了方便后序推导，把成像平面当做一个虚拟的成像平面——“归一化成像平面坐标系”，即光芯到平面的距离归一化为1，即f==1，这个1是个无量纲的数值。你把上述(2)式子中的所有f全部替换成1即可，便有(3)式：

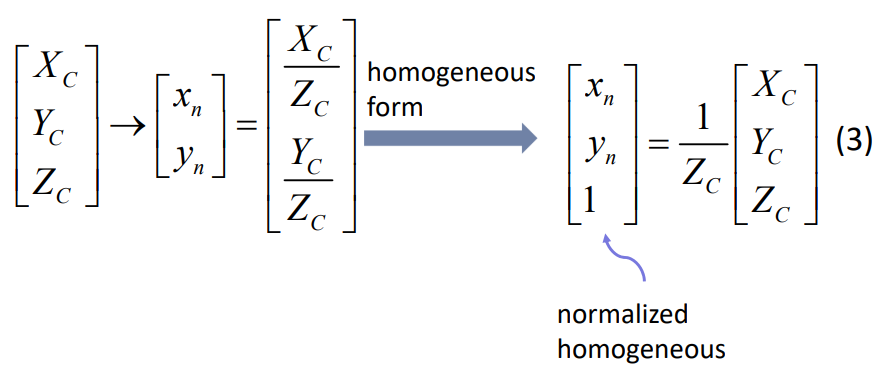
我还要补充说明一点(结合下面的最终模型连续矩阵乘法，且我们先忽略掉扭曲参数s)， $\lbrack x_n,y_n,1 \rbrack$ 是归一化成像平面坐标系下的坐标，n表示norm。诶你说不对啊，归一化成像平面坐标逻辑上说应该是由成像平面坐标来的，但 $\begin{bmatrix} f&0&0\\ 0&f&0\\ 0&0&1 \end{bmatrix}·\frac{1}{Z_c} \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}$ 才是得到成像平面坐标，你 $\frac{1}{Z_c} \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}$ 这个式子都不够完整，怎么能说是得到归一化成像坐标呢？事实上， $\begin{bmatrix} f&0&0\\ 0&f&0\\ 0&0&1 \end{bmatrix}$ 反正被简化成了单位阵，归一化坐标的算是当做是一种简化写法即可。同样的，后面有像素坐标算式 $\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \begin{bmatrix} f_x&0&c_x\\ 0&f_x&c_y\\ 0&0&1 \end{bmatrix}· \begin{bmatrix} x_n\\ y_n\\ 1 \end{bmatrix}$ ，你说不对啊，K是将成像平面坐标下的点转化为了像素坐标，上面说了，本来应该构成K的 $\begin{bmatrix} f&0&0\\ 0&f&0\\ 0&0&1 \end{bmatrix}$ 被从K里分离出去用以将成像平面坐标转化为归一化成像平面坐标，你这里怎么还能写K呢？你应该写成 $\begin{bmatrix} \frac{1}{dx}&\frac{tan \alpha}{dx}&c_x\\ 0&\frac{1}{dy}&c_y\\ 0&0&1 \end{bmatrix}$ 才对——但事实上，当f=1后，这种写法和正宗的K在数值上是等效的。所以，你就当做是：惯用表示形式上来看，在归一化成像平面坐标[xn,yn,1]转化成像素坐标的过程中(分两步，第一步得出归一化成像平面坐标，第二步得出像素坐标)，第一步用到的 $\begin{bmatrix} f&0&0\\ 0&f&0\\ 0&0&1 \end{bmatrix}$ 被借给了第二步，或者说，归一化成像平面坐标系直接发它当做单位矩阵省掉了。综上，从本质上来说，计算成像平面坐标不仅用到了外参[R t]，还用到了内参 $\begin{bmatrix} f&0&0\\ 0&f&0\\ 0&0&1 \end{bmatrix}$ ，只不过把成像平面坐标系退化成归一化成像平面坐标系后，该内参就当做是完全省掉了。
上述得出来的(x, y)是在成像平面上的连续坐标，而非离散的像素坐标，我们要离散的像素坐标。要注意到的是，成像平面不一定是一个矩形，有可能是一个平行四边形；成像平面一个像素的长宽被设为dx、dy：
于是我们终于得到了从3D世界坐标系到2D成像平面坐标系到像素坐标系的变换模型，总结上面几步，可以得到以下总模型，漂亮：

看看这个漂亮的模型 $u = 1/Z_c \times K_{3\times 3} \times [R t]_{3\times 4} \times P_{4\times 1}$ ([R t]把世界坐标系转化成相机坐标系，1/Z、K一起将相机坐标系转换到像素坐标系。事实上，u还有一步取整操作)。其中：
- Zc是被pc=[R t] * pw计算得来的(注意pw是齐次坐标)，Zc同时反映了物理点在世界坐标系中的坐标及离线外参
- 而K确定无疑反映的是相机内参(其中cx、cy是光芯投影在像素坐标系上的坐标，量纲是像素，s刻画了两个坐标轴的不垂直性，称为“扭曲参数”，matlab工具包会考虑s，Opencv不会，且现代相机都可以把s近似为0——所以我们后面的论述中将不考虑s！)
- [R, t]毫无疑问反映的是离线外参。
还要注意K中参数都是以像素为单位，例如f单位是毫米，则dx单位为毫米/像素，所以fx的单位是像素。

于是，一个相机的成像原理模型，我们可以毫无疑问地说它是由相机内参与离线外参决定的，我们标定出了内参与外参，就能找出成像平面上的离散像素点与世界坐标系中物理点的相互关系。而我们要先标定出容易标定的内参，去畸变，即可将本来难以标定的外参也变得好标定，所以内参标定一方面使得建立模型；一方面帮助外参标定。

引入镜头畸变的相机成像模型：

我们不考虑成像平面的扭曲系数s。

镜头畸变分为两种，径向畸变和切向畸变。径向畸变是由于光线在透镜边缘的弯曲程度大于透镜光学中心的弯曲程度所引发的，切向畸变是用于镜头平面与成像器件平面不严格平行时所发生的。径向畸变分为正/负两种，分别称为枕形畸变和桶形畸变。

我们之前讲的针孔成像相机的成像原理从世界坐标转化为归一化成像平面坐标的公式 $\frac{1}{Z_c}\left[ R\quad t \right]_{3\times 4} \begin{bmatrix} X_w\\Y_w\\Z_w\\1 \end{bmatrix} = \begin{bmatrix} x_n\\y_n\\1 \end{bmatrix}$ 依然在这里适用，我们考虑镜头畸变，是在归一化成像平面坐标系下对[xn,yn,1]进行建模。

考虑到径向畸变，有模型： \[ \displaylines{ x_dr = x_n (1+k_1 r^2 + k_2 r^4 + k_3 r^6) \\ y_dr = y_n (1+k_1 r^2 + k_2 r^4 + k_3 r^6) } \] 考虑到切向畸变，有模型： \[ \displaylines{ x_dt = x_n + (2\rho_{1} x_n y_n + \rho_{2}(r^2 + 2x_n^2)) \\ y_dt = y_n + (2\rho_{2} x_n y_n + \rho_{1}(r^2 + 2y_n^2)) } \] 结合起来，有模型： \[ \displaylines{ x_d = x_n (1+k_1 r^2 + k_2 r^4) + 2 \rho_{1} x_n y_n +\rho_{2} (r^2 +2 x_n^2) + x_n k_3 r^6 \\ y_d = y_n (1+k_1 r^2 + k_2 r^4) + 2 \rho_{2} x_n y_n +\rho_{1} (r^2 +2 y_n^2) + y_n k_3 r^6 } \] 其中$k_1$、$k_2$、$ρ_1$、$ρ_2$、$k_3$称为相机的畸变参数，它们当然也是相机的内参数。

于是，针孔相机成像模型 $u=\frac{1}{z_c}K\left[ R_{3\times 3}\quad t_{3\times 1} \right]p_w$ 变成了 $u=K·\textit{D}\{ \frac{1}{z_c} \left[ R\quad t \right]_{3\times 4} p_w \}$ ，D是畸变算子(非线性变换没法用线性代数的矩阵乘法表示)，其参数即是畸变参数，和K一同时相机内参数，和K一道将归一化成像平面坐标转化为像素坐标(要注意的是，K的组成部分(f,f,1)本来是用来算成像平面坐标的，作为K的一部分成为针孔相机全部内参，但由于这里要求归一化成像平面坐标，它是单位阵就被在数学形式上省掉了，但它实际上是在哪起作用你要知道)，K是像素化，D是加畸变。

畸变镜头内/外参标定：

按道理来说，我们一般都是要先标定内参再标定外参，但实际上，对于模型$u=K \times D\{ 1/Z_c \times [R\quad t] \times pw \}$，我们完全可以把内外参放在一起标定，很简单啊，你找到一组样本点(u,pw)，套入该模型，然后开始凸优化即可，这里的凸优化不像我们在图像拼接的点对匹配那里用的最小二乘法那么简单了，这里可能要用到SGD。

好了，你知道你要取样本点然后凸优化成像模型了，那么问题来了，模型$u=K \times D\{ 1/Z_c \times [R\quad t] \times pw \}$的参数除了K和D的9个参数外，还有R，t的参数要优化，t还好说，旋转矩阵R的参数就太多了啊，你要引入保持R正交的约束，凸优化太麻烦——但是我们有方法把R的参数用另一种表示方法降维。我们知道R代表的旋转矩阵在3D空间中共有3个自由度，实际上我们可以用3D空间中一个向量来表示这个旋转，这叫3D欧氏空间旋转的轴角表示，即该向量有两个元素：旋转轴和角度，点绕旋转轴逆时针旋转，旋转的角度$\theta$是旋转轴的长度。注意$0\leq \theta \leq \pi$，也就是说，你不可能绕着这个旋转轴顺时针转，也不可能转动超过180度，于是该轴角代表的旋转变换就有一个180度的盲区，这个盲区怎么解决？你把旋转轴倒个方向不就行了呗。

所以，我们完全可以用“罗德里格斯公式”将9个参数(实际上自由度只有3，我想应该是这个矩阵的其他值都可以被迹上的元素所确定)的旋转矩阵R转变为3个参数的轴角d，而R的表示为R(d)。我们就可以用$u=K \times D\{ 1/Z_c \times [R(d)\quad t] \times pw \}$表示畸变相机成像模型了，参数量只有15个，也不需要正交约束。

问题又来，如何将R转变为轴角d？角度好说，有现成公式$\theta = arccos \left( \frac{tr(R)-1}{2} \right)$。旋转轴方向也好说，也有现成公式$R\textbf{n}=\textbf{n}$，意思就是说R对应的特征值为1的单位特征向量就是旋转轴。但是在计算旋转轴是，我们有3个问题：

R一定有特征值1吗？数学上肯定有
1个特征值会不会对应多个线性无关的特征向量？可能会，要是如此，则R的3个特征值都会为1，则theta=0，则不旋转
若是特征值1对应的特征向量确实只有线性无关的一个，但它可以有两个相反的方向啊，该选哪个？我们上面说了，一个轴角有180度的盲区，两个相反旋转轴盲区互补，我们看看哪个方向的旋转轴能通过罗格里斯公式转换为R即可，我们通过验证的方式选择选取哪个方向的旋转轴。

综上，我们要做凸优化的表达式为： \[ \Theta^{*}=\mathop{\arg\min}\limits_{\Theta} \sum_{i=1}^{m} \sum_{j=1}^{n} \frac{1}{2} \left\Vert K \cdot \textit{D} \lbrace \frac{1}{z_{cij}} \left[\textit{R}(d_i)\quad t_i\right]p_j \rbrace-u_{ij} \right\Vert_2^2 \] 优化参数集合为： \[ \Theta = \lbrace f_x,f_y,c_x,c_y,k_1,k_2,\rho_1,\rho_2,k_3,\lbrace d_i \rbrace_{i=1}^m, \lbrace t_i \rbrace_{i=1}^m \rbrace \] 其中内参是普适不变的，外参是随着拍照角度变化的。其实最后我们要给图像去畸变，只用得上内参，而且由于每张照片的外参都不一样，所以最终优化出来的外参基本也没啥用，你用张正友标定出来的相机外参只适合棋盘格作为世界坐标系的情况，我们在做鸟瞰视图或者单目测量的时候，实际上选用的世界坐标系坐标原点应该是相机本身所处位置，所以我们还必须得重新用去畸变的图像和世界平面坐标系的点对关系来确定新的[R t]，这是一个射影变换矩阵，我们只需要解决线性最小二乘问题就能得出[R t]了，具体参见图像拼接知识点。那么，这里在标定相机内参的时候为什么还要将相机外参一起优化呢？因为它们是在同一个模型里啊！相互影响，一个是准确的，才能让模型中另一个参数也准确。

m代表采样的照片个数，n代表一个照片上的像素的个数。采样的时候，你从不同角度对一个张正友棋盘格拍m张照片，于是pj代表棋盘格确定了世界坐标系下的棋盘格上的点，且由于世界坐标系有棋盘格所确定，所以棋盘格上的pj下标不随n而改变。而一张照片确定一个旋转R，所以di的下标只随着m而改变。但由于z由R和pj同时确定，Z=[R t]*pw,所以下标随m和n改变。

然后你有一个问题了，为什么我们要拍多张照片？我们直接拍一张照片不好吗？一张照片上的样本点n够多了啊。我们可以这样来理解，之前我们讲射影变换时讲过，一张照片，真实坐标到图像坐标是一组同样的射影变换，一组同样的射影变换上的4个2D点对(一共能列8个线性无关方程)能确定8个自由度，再来更多的n>4个点对也最多只能确定8个自由度而已，这是有两个平面确定的唯一射影变换的性质本身所决定的。但我们这里的相机成像模型，对于每一张照片，一共有9个内参，6个外参，其中内参不论对于哪张照片来说都一样，外参则是不同照片不一样，但是一张照片只能确定8个自由度，远不及这15个参数。那要是我们拍两张照片呢？一共有21个参数要确认(15+6)，但也只能确定16个自由度，还是不够。要至少5张照片，一共39个待优化参数，能确定40个自由度，够了！这里我们把m>5取得越大越好，这是为了使得凸优化更准确，就像是图像拼接那里求线性几何变换矩阵H，你8个方程虽然能是能确定8个自由度，但其实方程也是不一定有解的，你只是要最小化误差而已，而你取的样本点越多，你就能兼顾所有样本点，让它们在线性变换H后离真实值的误差都达到最小——所以这里取m>5，也是为了求得一组内参值，使得这组内参(外参随着不同m，即不同拍照角度而变化)再所有拍照角度下都能尽量使得模型更精准，pw模型u中pw和u的误差更小。

假如不考虑畸变参数的话，那么只需要2张照片就够了。

参数初始化：

那么，你该怎样优化公式 $\Theta^{*}=\mathop{\arg\min}\limits_{\Theta} \sum_{i=1}^{m} \sum_{j=1}^{n} \frac{1}{2} \left\Vert K \cdot \textit{D} \lbrace \frac{1}{z_{cij}} \left[\textit{R}(d_i)\quad t_i\right]p_j \rbrace-u_{ij} \right\Vert_2^2$ ？

首先一点，这个公式很难优化，你要先确定初值，然后去迭代优化。初始化实际上就是给各个待优化参数估计一个值，这个值接近其最优解，以此来减少迭代优化时的计算量。

初值怎么确定？

你看待优化参数有 $\Theta = \lbrace f_x,f_y,c_x,c_y,k_1,k_2,\rho_1,\rho_2,k_3,\lbrace d_i \rbrace_{i=1}^m, \lbrace t_i \rbrace_{i=1}^m \rbrace$ ，其中畸变参数我们没好的初始化方法，先给它初始化全为0(相当于退化成一个针孔成像模型了)，然后主点坐标cx，cy本来代表光芯投影在像素坐标系，可以取初值分别为成像平面宽高的一半(单位为像素)，而fx、fy的初始化就复杂了，我们要通过构建一个关于K的方程，然后在该方程中把K解出来(K中的cx、cy初值已经确定了)。如何构建这个关于K的方程，科学家想到了一个利用消失点算法。

我先介绍消失点的概念和性质——请注意，此时我们把畸变参数都初始化为0了，相机退化成了针孔成像模型，即： \[ \textbf{u}=\frac{1}{z_c}K\lbrack R_{3\times 3}\quad t_{3\times 1} \rbrack \textbf{p}_w \] 我们下面讲消失点也是在针孔成像模型体系下讲的。退化成无畸变的成像模型后，成像平面和物理平面之间也就满足射影变换了，也能求出单应矩阵了——而且你还要注意的是，表征成像平面与物理平面之间射影变换的单应矩阵H变换的是两个平面上的2D齐次坐标，而不是u=1/Zc * K * [R t] * pw中的3D齐次坐标pw到2D齐次坐标u。

消失点：

消失点的文字概念我不多讲，它就是物理世界中一条直线的无穷远点在成像平面坐标系下的投影，你看下图即可知消失点：

消失点_1

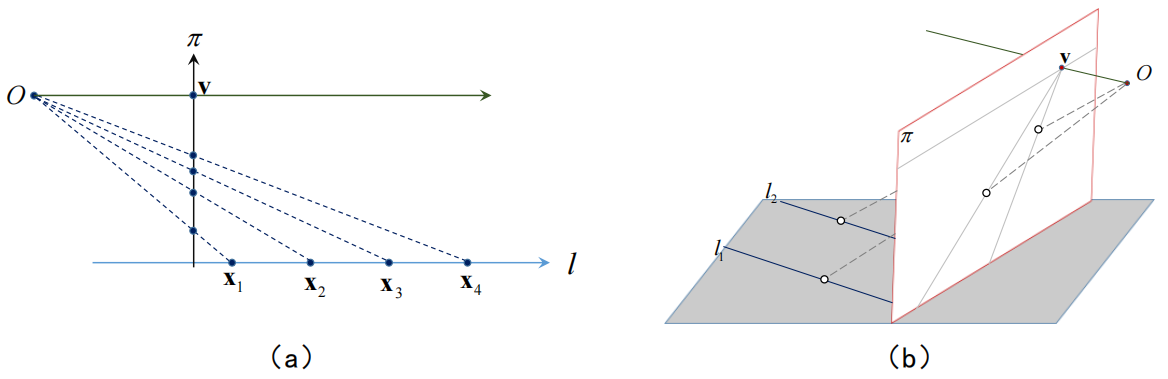
其实我们逆向思考，可以发现成像平面上任一个点v都是消失点，对应于物理世界中与Ov平行的直线。

很有意思的一点是，你自己在画图时可以这么确定消失点：只需要过光芯O，作一条与目标直线平行的直线，其与成像平面的交点v即是物理世界中直线的消失点。故而你易知：

由光芯位置+成像平面大小+直线方向决定了，一条直线不一定能在成像平面上取到消失点；
成像平面上某个消失点对应的物理世界中的直线方向平行于光芯到该消失点的方向向量，该方向向量即是该消失点在成像平面坐标系(就算不是归一化成像平面坐标系也没关系，但当然了，我们现在把成像平面坐标系都当做归一化成像平面坐标系了)下的坐标(未经K变换到像素坐标系)，即为1/Zc * [R t] * pw，pw代表了物理世界中对应直线的无穷远点；
由于消失点对应的物理世界中的直线的方向向量就是该消失点在归一化成像平面坐标系下的坐标，我们可以得知，物理世界中对应直线的方向向量不仅可以表示为v=1/Zc * [R t] * pw，还可以表示成v=K^-1 * u，u是像素坐标系下的消失点坐标，后一个式子表示明显比前一个好，因为1/Zc * [R t] * pw需要得知[R t]，其未知且与我们最终要初始化的fx和fy无关，而v=K^-1 * u虽然K未知，但K中的cx、cy已知，且fx、fy是我们待初始化的参数，当然其实现在u你还是未知的，因为你不知道物理世界中一直线的无穷远点究竟映射到像素坐标系下的哪一个像素，但是没关系，我下面会讲述如何得到u的，是要通过计算，而非通过观察照片上的像素。再强调一遍，v既是消失点归一化成像平面坐标，也是方向向量。

于是科学家发现，对于v1和v2代表的直线的方向，若是v1垂直与v2，则有点积式子： \[ u_1^T \times (K^{-T} \times K^{-1}) \times u_2 =0 \] 多漂亮！多破局的一个等式啊！cx、cy你知道了，你要估计fx、fy的值，你这里只需要找到两组垂直直线的像素坐标u1-u2、u3-u4即可，为什么一定要两组垂直直线？因为你fx、fy有两个自由度，你一组直线带进去只能得出一个等式解决一个自由度。然后，你要怎么得到u1、u2呢？我是说，你怎么知道像素坐标系下某个像素点的坐标对应于物理世界中哪条直线呢？唉，你想，要是我找到归一化成像平面上的坐标v就好了，它们的坐标就是物理世界中直线的方向向量嘛，我说对啊，可惜你得到v需要K啊，你要是知道K了你还估计什么fx、fy？所以，抛弃那种无意义的想法，好好想想，如何得到某个u和物理世界中某条直线的对应关系。如何？你不知道像素坐标对应于哪条直线的无穷远点对吧，但你直接可以根据棋盘格知道物理世界中无穷远点的坐标啊！棋盘格定义的物理世界坐标系是3D的，我们这里暂且简化点，说它棋盘格2D平面上的无穷远点齐次坐标，典型的不就是(1,0,0)、(0,1,0)、(1,1,0)、(1,-1,0)吗。然后，我们假设了这里是针孔成像模型，你已经知道了棋盘格平面上的点的2D物理坐标pj-inf，你也知道了像素坐标系下对应点的2D坐标uj，而这两个平面之间是满足射影变换的，你完全可以用图像拼接一章中的最小二乘法求出两个平面间的单应矩阵H(为什么我们要把物理世界上的无穷远点在2D物理平面上表示呢，就是为了方便求两个满足射影变换关系的平面之间的单应矩阵H。你可能还会有疑惑，为什么物理世界下的连续坐标$p_{j\infty}$会和像素坐标系下的离散坐标uj间能建立单应矩阵？我也不知道，我感觉能)，然后将物理平面上的无穷远点(1,0,0)、(0,1,0)、(1,1,0)、(1,-1,0)变换到像素坐标系下，你便得到了u1、u2、u3、u4！好耶！

对于等式$u_1^T \times (K^{-T} \times K^{-1}) \times u_2 =0$，你终于得到了u1、u2，你可以解fx、fy！解法其实有点复杂，我不讲，你自己看书。

现在，对于优化$\Theta = \lbrace f_x,f_y,c_x,c_y,k_1,k_2,\rho_1,\rho_2,k_3,\lbrace d_i \rbrace_{i=1}^m, \lbrace t_i \rbrace_{i=1}^m \rbrace$，你初始化了所有内参，你如何初始化外参d、t？

初始化外参d、t，我们现在来推导。

设pwj=(x,y,z,1)是物理世界上的3D齐次坐标，且是棋盘格上的坐标，则其z=0，实际上pwj=(x,y,0,1)。pj=(x,y,1)是对应的，物理世界棋盘格平面上的2D齐次坐标。

由uj=K * 1/Zc * [R t] * pwj且vj=1/Zc * [R t] * pwj且vj是齐次坐标，可知Zc * vj=[R t] * pwj=[r1 r2 r3 t] * pwj成立，而由于pwj的z=0，所以有pwj’=(x,y,1)，且Zc * vj=[r1 r2 t] * pwj’成立。

对于上面同一组(uj,vj)，又由前文中估计fx、fy过程中所得知的：vj=$K^{-1}$ * uj与uj=H * pj可知vj=$K^{-1}$ * H * pj，同时，由于vj是齐次坐标，所以c * vj=$K^{-1}$ * H * pj=P * pj成立，显然在估计fx、fy的过程中，你已经能知道P了。

对比公式Zc * vj=[r1 r2 t] * pwj’与公式c * vj=P * pj，你会发现P和[r1 r2 t]实际上是将物理世界中的同一个点pwj’=pj变换到成像平面坐标系下同一个点vj，而P是我们在估算fx、fy时算出来的，P和[r1 r2 t]之间实际只相差一个实数倍，这个实数倍的相差在Zc和c的差别上体现出来。你要是能算出这个实数倍来，就能由P求出[r1 r2 t]，再由R=[r1 r2 r3]的正交性质由r1、r2算出r3来，这个倍数关系好算，用于R=[r1 r2 r3]是正交的，所以$\left\Vert r_1 \right\Vert = \left\Vert r_2 \right\Vert = 1 = \lambda \times \left\Vert P_1 \right\Vert = \lambda \times \left\Vert P_2 \right\Vert$，我们要算$\lambda$，opencv在实现这一步时，如是做：$\lambda=2 / (\left\Vert P_1\right\Vert + \left\Vert P_2\right\Vert )$，为什么不直接取$1/ \left\Vert P_1\right\Vert$或$1/ \left\Vert P_2\right\Vert$，这是因为P本来就是由K和H估算出来的，本来就不一定遵守$\left\Vert P_1\right\Vert =\left\Vert P_2 \right\Vert$。于是现在，$\lambda$你知道了，[r1 r2 t]自然也就知道了，[r1 r2 r3 t]自然也知道了，于是[R t]就知道了，运用罗德里格斯公式，d和t自然就知道了。

到目前为止，$\Theta = \lbrace f_x,f_y,c_x,c_y,k_1,k_2,\rho_1,\rho_2,k_3,\lbrace d_i \rbrace_{i=1}^m, \lbrace t_i \rbrace_{i=1}^m \rbrace$ 全部初始化完成。接下来，你要根据某种算法迭代优化这些参数，待优化公式是： \[ \Theta^{*}=\mathop{\arg\min}\limits_{\Theta} \sum_{i=1}^{m} \sum_{j=1}^{n} \frac{1}{2} \left\Vert K \cdot \textit{D} \lbrace \frac{1}{z_{cij}} \left[\textit{R}(d_i)\quad t_i\right]p_j \rbrace-u_{ij} \right\Vert_2^2 \] 你要通过怎样的算法来优化给公式？接下来讲解非线性最小二乘，我们这里的非线性最小二乘刚好是一个无约束的优化问题。

非线性最小二乘：

对于问题： \[ \textit{F}(x)=\frac{1}{2}\sum_{i=1}^{m}(f_i(x))^2 = \frac{1}{2} \lbrack f_1^2(x)+f_2^2(x)+…+f_m^2(x) \rbrack \] 我们要优化参数x使得F(x)最小。当f(x)可以用线性函数Ax+b的形式表达式，它就是一个线性最小二乘问题，当不能时，就是一个非线性最小二乘问题，“非/线性”、“最小”、“二乘”这几个词都有其实际意义。

对于带优化非线性函数f(x)，我们要找一个自变量值x，使得f(x)在它的定义域上(由于非线性最小二乘往往是无约束优化问题，所以默认定义域为Rn)取得最小值(有时候也可能要f(x)的最大值，这时候我们就f(x)=-f(x))，这个时候x就是最优解，而且由于难以找到x=argmin f(x)的闭式解，我们求得的x往往是局部最优解。

我们首先要知道如何判断一个点x上的f(x)是否是最优解(argmin f(x))？我们看看f’(x)是否等于0，等于0就是驻点，驻点有可能是最优解，但不一定，因为驻点可能是argmax f(x)，且马鞍面也有驻点，所以我们要用海森矩阵来判断。考虑到以下泰勒展开： \[ \textit{F}(x+h)=\textit{F}(x)+h^T F^{‘}(x)+\frac{1}{2}h^T F^{“}(x)h + \textit{O}(\left\Vert h \right\Vert^2) \] 当这里的海森矩阵是正定的时候，x是局部最小解；当它是负定的时候，x是局部最大解；当它不确定是，x是鞍点。鞍点这种情况很特殊，我们在迭代更新模型参数的时候就不考虑鞍点了。

我们现在知道如何判断一个解x是否是局部最优解了，前文也得知x的初值了，然后我们要做最主要的工作是不断更新初值x，使最终的x成为局部最优解。

更新x的策略就只有“下降法”(下降的是F值)，下降的参数是h和alpha(2步法没有alpha)，每次迭代时，h都有解析解。相比于alpha的取值，h才是重中之重。

下降法实施过程中要时刻遵守的基本准则是：$f(x)_{k+1} \lt f(x)_{k}$。注意：在2步法中，这不意味下降方向h使得f下降就行，还要考虑下降的距离alpha，因为可能$h\times f(x)^{'}\lt 0$，但是alpha太大，使得最后的$f(x)_{k+1}$ 反而$> f(x)_k$ 。当然，两步法中先求h时，我们暂且先考虑h满足$h\times f(x)^{'}\lt 0$理想使得f下降即可，考虑alpha的取值是否合理是在线搜索里做的。

下降法也分两种策略，一种是2步法，先找到下降的方向，再确定下降的距离；另一种1步法，是把下降的方向和距离一起找。

我们先说2步法。

2步法的第一步有Steepest descent method、Newton’s method、SD and Newton hybrid，找下降距离的方法有line search。

非线性最小二乘_1

Steepest descent method：是每次更新时都找最陡的下降方向，点x处最陡的下降方向就是-F’(x)，证明如下：

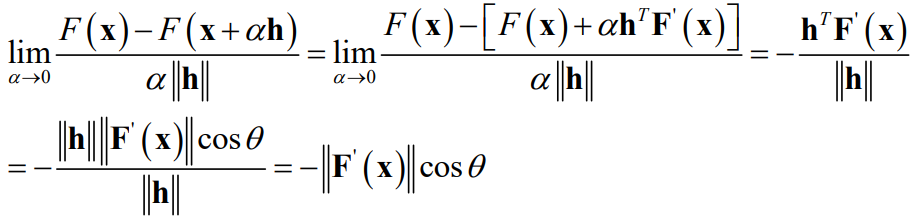
非线性最小二乘_2

h代表下降的方向，alpha是一个很小的正数，代表下降的距离(在后面由线搜索得到)，$\lim_{\alpha \to 0}\frac{(F(x)-F(x+\alpha\times h))}{(\alpha\times \left\Vert h\right\Vert)}越大，h方向下降得越陡峭。theta是下降的方向与F’(x)的夹角，可以知道当夹角为$\pi$$时，下降得最陡，这个时候下降方向h=-F’(x)。

由此我们得到了一个重要结论，只要移动方向h和该点导数F(x’)的内积小于0，则h方向必然是下降的。这可以用来验证一个

最陡下降法往往只在更新x的初始阶段效果最后，在更新后期的时候，Newton’s Method效果好，我们下面介绍一下牛顿法。Newton’s method为什么在最终阶段表现良好？你看了下文就知道。

Newton’s Method：

牛顿法的核心思想是，在f(x)处，我们想找到这样一个方向h，往它走一步，最有可能到达驻点，即f’(x+h)=0。于是我们固定x不动，近似求解这样一个h，使得f’(x+h)=0，它是局部最小值。

前面说了，我们就不考虑极特殊的鞍点，这里，我们也不考虑f’(x+h)=0时f(x+h)是局部最大值的情况，两步法中，我们先求下降方向h，我们只在意h方向在不考虑alpha取值的情况下理想能让f值下降即可(取不取得到局部最大值是alpha干预的事情，h管不了，而线搜索才算alpha，而且我觉得线搜索算出来的alpha是想让alpha不会太大到使得$f(x)_{k+1} > f(x)_k$，应该也不会太管局部最大值的事情把？)。反正我们这里求h也是近似求法，f(x+h)还不一定是个驻点呢，你在求h的时候难道还要计算一波x+h处的海森矩阵是不是正定的吗？肯定不会。

如何由$f^{'}(x+h)$近似解出$h$，采用一阶泰勒展开近似：$f^{'}(x+h)=f^{'}(x)+f^{"}(x)\times h=0$，继而解得$h=-1\times f^{"}(x)^{-1}\times f^{'}(x)$。

但前面说了，我们只要且必须要关心h的是不是下降方向，这只需要我们判断h方向是否和f’(x)方向相反即可，此时根据f’’(x)h=- 1f’(x)可知只要f’’(x)是正定的就行。

于是这就凸显出了Newton’s method的弊端，作为两步法的一部分，它只有在x的海森矩阵是正定时才有用，不想Steepest descent method，在如何x处都有用。但Newton’s method用了二阶导的信息，它收敛速度通常比Steepest更快，特别是在后期即将达到局部最小值的情况下，此时海森矩阵通常都是正定的(一阶导逐渐变大)，它表现得很棒。所以在实际情况下，我们通常建立一种混合Newton和Steepest的method，叫做SD and Newton hybrid。
SD and Newton hybrid：

由于Newton’s method只有在海森矩阵正定时才有用，但是它效果又是那么的好，于是我们有了下面算法：

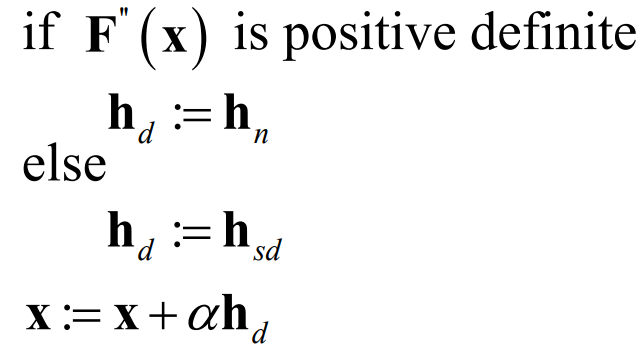
于是上述，你2步法第1步找到下降方向了，继而找下降距离用线搜索line search，line search老师没讲。

下面来讲讲1步法。

1步法可分为两种实现，Trust Region method和Damped method，但它们本质相同，它们的本质在于，对于待优化函数F(x)而言，找到x点一个函数(张林戏称为“拐杖”)L(x)，这个函数是一个二次凸函数，能较好地模型F(x)在x附件的形状，我们主要找到足够二次凸函数的最小值点就是本次迭代过去的新x值了，这个L(x)的形式为： \[ \textit{F}(x+h)\simeq \textit{L}(h) = \textit{F}(x)+h^T c + \frac{1}{2} h^T Bh \] 不同的x处有不同的参数F(x)、c、B所构成的L(h)的形式，也就有了不同的h解值。

h既是迭代去新值的距离，又是方向。c是一个向量。B必须是一个对称阵，但我不明白它为什么得是一个对称阵，是因为只有当它是对称阵时L(h)才是一个类二次凸函数的函数吗？那么B应该是正定的啊，我不明白，我想问老师。

最简单的拐杖函数L(h)的求法是直接对F(x+h)做泰勒展开。

但是，这样的一个拐杖函数L(h)不一定拟合F(x+h)拟合得准确，依据L(h)求出来的局部最小值可能是错的，即使得$F(x_k+1) > F(x_k)$，特别是当求出来的h特别大的时候，局部最小值最有可能是错的。我们有两个方案能缓解这种现象，一种叫做Trust-region method，一种叫Damped method。TR和D这两种方法更像是对更新的h的一种约束策略，而非一种具体的1步法，不像是我们讲2步法时SD、N、SD-N、LS，都是很具体的方法。毕竟，L(h)的具体形式没有确认。你可以看出来的是，TR法和D法其实本质也是同样的约束策略，只不过后者是一种软性约束，前者是硬性的，软性约束更优美好算，实际情况中也用的更多，我们下面在具体说明某种确定了L(h)形式的1步法时，用到的约束策略都是D法。

Trust-region method：

给h硬性设定一个取值范围$\Delta$，h的计算式子变成了： \[ h_{tr}=\mathop{\arg\min}\limits_{h}\textit{L}(h),\, s.t., \, h^Th\leq \Delta^2\quad \textbf{(Eq.1)} \] 算法为：

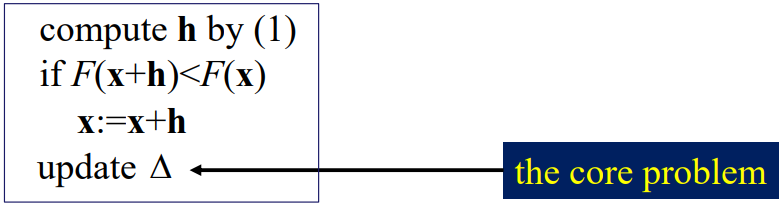
每轮迭代后，都要根据h迭代的效果更新$\Delta$，如何量化迭代的效果？增益比。计算式如下：

依据$\Rho$更新$\Delta$的方式可以如下：
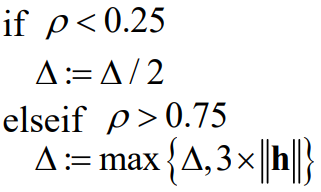
Damped method：

给L(h)增加一个针对h过大的惩罚项，h的计算式子变成了： \[ h=h_{dm}\equiv \mathop{\arg\min}\limits_{h}\lbrace \textit{L}(h) + \frac{1}{2}\mu h^T h \rbrace \quad \textbf{(Eq.2)} \] 于是h就有解析解$(B+\mu I)$正定时才有解： \[ h_{dm}=-(B+\mu I)^{-1} c \] $\mu$也跟$\Delta$一样，在每轮迭代$h$后要要更新，更新也是依据的增益比$\rho$：

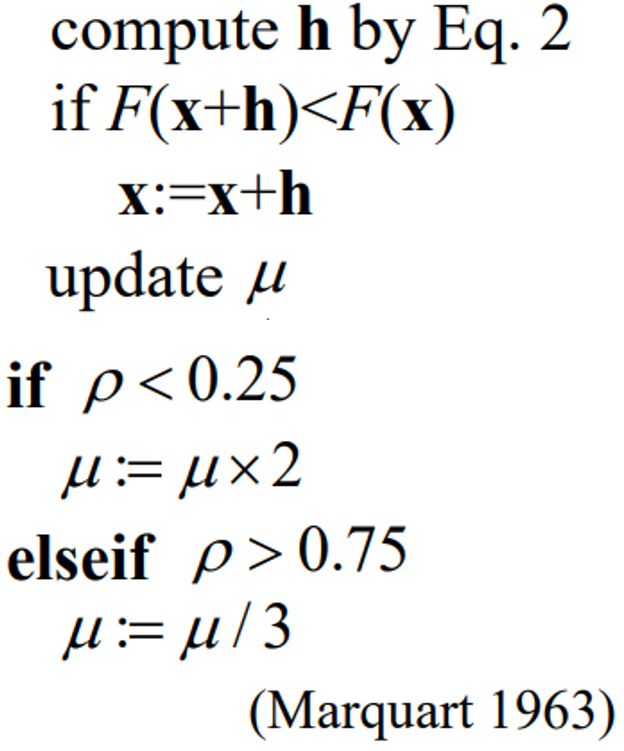
上述更新$\mu$的方法属于Levenberg-Marquardt算法的一部分，Levenberg-Marquardt也是一种1步法，它是阻尼法的一种，我们前面讲的阻尼法和信赖区域法都是基于一个拐杖函数的，但拐杖函数的具体形式我们没确定，LM算法就是把拐杖函数确定为了Guassian-Newton(alpha=1)法+阻尼因子。LM算法我们下面会介绍。

前面说了，要是我们把$L(h)$设为$F(x+h)$的泰勒展开的话，那么就会得到$L(h)=F(x)+h^T \times F^{'}(x)+\frac{1}{2} \times h^T \times F^{"}(x) \times h$，于是我们上面提到的h的解析解的形式就变成了($F^{"}(x)+\mu\times I$正定时才有解)： \[ h_{dn}=-(F^{“}(x)+\mu I)^{-1}F^{‘}(x) \] 我们管这种具体化L(h)函数为F(x)泰勒展开的Damped Method为阻尼高斯法，其实我们可以看出一个起名字的规律啊，当我们一用到海森矩阵，那么指定方法的名字必然带“Newton”，而这里的阻尼高斯法是采用阻尼约束策略的1步法，所以叫做阻尼高斯法。

有一个很有意思的现象，对于Damped Neweton’s method，若是你将Mu置为很大，则它退化成了Steepest Method，若是你将Mu置为很小，则它退化成了Newton’s method，这两种情况下h都只代表方向，所以你可以窥见：对于1步法而言，我们往往把h当做包含了方向和距离，但其实你乘一个alpha表示距离也没关系，对于下面要将的Guassion-Newton法就是这样的。所以1步法和2步法没有本质区别，1步法只不过是alpha为1的2步法罢了(你非说的话，可以讲用了拐杖函数L(h)并且把alpha取1的都叫1步法)。你可以从1步法中的阻尼法中的阻尼牛顿法的退化，以及Guassion-Newton法的alpha中窥见出来。

总结上述1步法和2步法，你能看出它们界限很模糊，我们下面来讲一个Guassion-Newton method，进一步模糊它们的界限。

上述将的SD法效果不好，Newton法和D约束策略的具体D-Newton法(一般不用硬性的TR法)都要求海森矩阵，但对于一个具体的非线性最小二乘问题$F(x)=\frac{1}{2}\times f(x)^T\times f(x)$而言，求它的海森矩阵是很贵的，不信你自己算一下，公式形式很复杂的。例如对于由m个样本聚合成的待优化函数F(x)，共n个待优化参数，它的海森矩阵是：

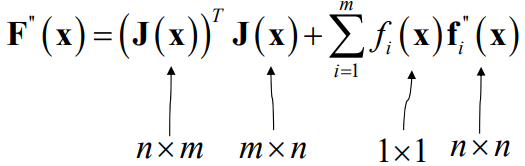
非线性最小二乘_8

所以上述讲的具有实用价值的SD、SD-Newton、D-Newton法(line search找alpha，不如h重要)都是讲着玩的理论，一般情况下都不使用。我们一般都是用Guassion-Newton法。

GN法是上述1步法中，但它没有对h采用任何约束，它很naive。它和DN一样，具体了L(h)函数，不过它的L(h)函数不是直接对F(x+h)泰勒展开，而是将f(x+h)泰勒展开后相乘，避免了复杂的海森矩阵计算，最终形式为： \[ \textit{F}(x+h)\approx \textit{L}(h) \equiv \frac{1}{2}(f(x+h))^T f(x+h)=\frac{1}{2}f^T f+h^T J^T f+\frac{1}{2}h^T J^T J h \] J指雅各比矩阵，海森矩阵是标量对向量的二阶导，雅各比矩阵是向量对向量的一阶导。

同样的，我们一开始就说过，所有h都有解析解(假设$J^T \times J$是正定的，即要求J是列满秩时，否则只能是半正定)，这里我不算了，很简单啊。

但是alpha=1时的GN法，1.作为1步法用了拐杖函数L(h)却没有用约束策略，很Naïve；2.而且在实用中，我们还要确定J是列满秩的，麻烦！所以我们第一步先引入阻尼约束，继而发现引入阻尼约束后，的L(h)=c+bh+ah^2的a必然正定，你可以证明。两个问题同时解决!所以，给GN法引入阻尼约束后的方法多么优美便捷，我们叫它Levenberg-Marquardt算法(同时也叫阻尼高斯牛顿法)。

Levenberg-Margqurdt算法的解析解： \[ h_{lm}=-(J^T J+\mu I)^{-1} J^T f \] 阻尼系数在每一轮迭代时可以用我们在阻尼牛顿法中提到的方法进行更新：

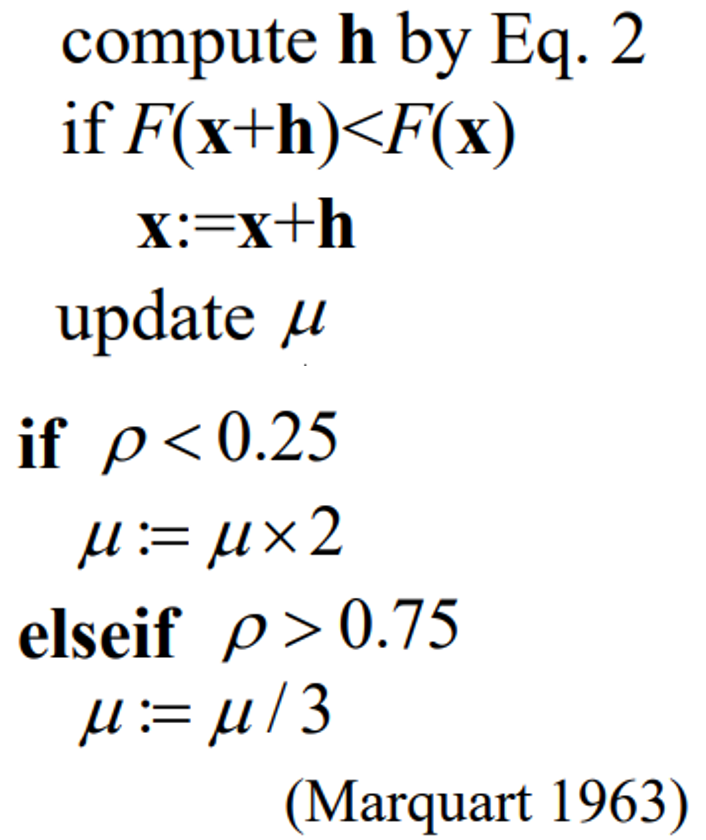
非线性最小二乘_9

综上，我们可以看到，DN法用的L(h)是对F(x+h)的泰勒展开，用了阻尼约束；GN法用的L(h)是对f(x+h)泰勒展开后平方，没用约束；LM法用的L(h)是对f(x+h)泰勒展开后平方，用了阻尼约束。它们都可以视作1步法，毕竟它们有1步法的特征：拐杖函数L(h)，且默认情况下alpha=1。

你可能会问：为什么我们在深度学习中直接用SGD？固定学习率？其实，SGD是对2步法中SD+LS的抽象，它完全继承SD，同时将LS简化为固定学习率(也不一定固定，你懂)，这样是为了简便alpha*h的计算，毕竟DL中参数那么多。我们在用以LM法为代表的传统参数更新法时，一般是在相机标定这样简单的任务中，而且一般求导得到Jacob矩阵都不是自动求导，而是符号求导，可能是为了更便宜吧。

我再总结一遍为什么我们最后要用LM法。因为SD效果不好，特别是在更新后期，Newton法效果好，但是要求海森矩阵，且海森矩阵必须正定，故而必须跟SD相hybird。DN也要求海森矩阵，且要求L(h)=c+bh+ah^2中的a必须正定。GN不需要求海森矩阵，但是它也要求L(h)=c+bh+ah^2中的a必须正定，且它没有阻尼约束，naïve。LM不需要求海森矩阵，在GN上引入有阻尼约束后，可证明L(h)=c+bh+ah^2中的a必然正定。

于是，你现在拿到了LM法，就用去优化非线性最小二乘问题 \[ \Theta^{*}=\mathop{\arg\min}\limits_{\Theta} \sum_{i=1}^{m} \sum_{j=1}^{n} \frac{1}{2} \left\Vert K \cdot \textit{D} \lbrace \frac{1}{z_{cij}} \left[\textit{R}(d_i)\quad t_i\right]p_j \rbrace-u_{ij} \right\Vert_2^2 \] 得到优化后的相机内外参。

于是，你现在有了完整的相机内外参数，以及一张畸变的照片ID，你要还原为无畸变的照片IB，你就利用无畸变照片上像素点xB到畸变照片像素点坐标xD的映射式子：xD=KD{(K^-1*xB)}，所以，去畸变只需要用到相机内参！外参R和t这里暂时用不上。然后你拿一张像素白板，通过上述式子将白板上的每个像素点映射到ID上，映射出来得到的ID上坐标肯定不是整数，所以要用插值法得到ID上像素值，于是，原来白板上的每个像素点都获取了像素值，你就能把白板变成IB了，你就成功去畸变了！

那么，我们为什么要反向思考用一张白板像素点映射到ID上获取白板上每个像素点像素值最终得到IB呢？我们为什么不直接将ID上的每个像素点直接映射到一个白板上得到IB呢？因为要是直接从ID上每个像素点映射到IB上，那映射得到的像素坐标肯定不是整数，你要插值吗？你要把一个像素值插值到周围4个像素点吗？太麻烦了，不如反向思考。其实很多地方都是同样的思想，你要通过一张图像I1得到另一张图像I2，你与其通过I1上像素点映射到I2上像素点，不如拿一张白板当做I2，然后每个像素点映射到I1上得到I2上每个像素值，这样的做法被使用在前面讲的图像拼接上，也被应用在下面要讲的鸟瞰视图生成上。

鸟瞰视图生成

得到了相机内参(标定阶段得到的外参全部丢掉不用)，你不仅能用于去畸变，你还能用于鸟瞰视图生成，鸟瞰视图也是一张2D图像。

鸟瞰视图生成：

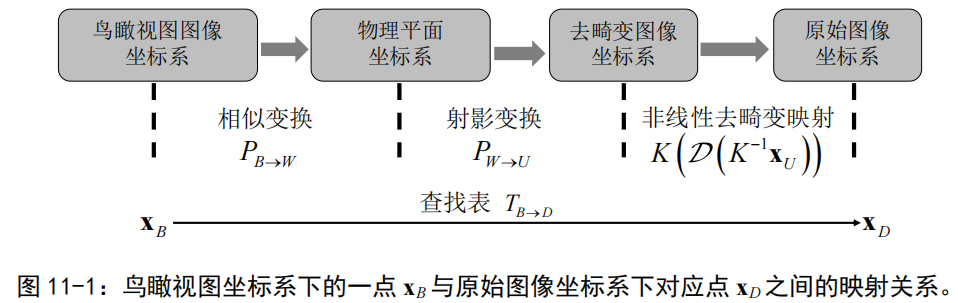
鸟瞰视图生成_1

上图你得到了鸟瞰视图上像素点到畸变图像上像素点的映射关系TBD。你还是利用前面讲过的反向思考，拿到一张白板，将白板上每个像素点映射到畸变图像上，插值得到像素值，然后获得白板上对应像素值，最终得到鸟瞰视图。其中，PBW的计算是我们没讲过的，但其实很简单，PBW是一个相似变换矩阵，你可以参考书上，建两个坐标系来算，很简单的。

要注意的是这里的物理平面坐标系并不是我们用张正友标定法标定相机参数时使用的物理世界坐标系，棋盘格确定的世界坐标系只是用来确定相机内外参用的，而最终也只有内参被用上了去畸变，外参则丢掉，因为优化出来的外参只适用于棋盘格世界坐标系。这里的物理平面坐标系的坐标原点被人为选取为相机本身所处平面位置，你要是选取其他坐标原点也行，PBW算出来就不一样了。但我觉得还是选取相机位置作为坐标原点会更好一点，更符合鸟瞰视图的常理。但要注意的是PWU是两个平面之间的射影变换阵，而不是相机外参，标定过程中涉及的相机外参[R t]自由度为6，表示物理3D坐标到相机光芯3D坐标之间的旋转平移变换，而这里的PWU自由度为8，表示两个平面之间的射影变换。毕竟，你张正友法用的物理平面坐标系坐标可以由棋盘格的位置任意确定，而这里生成鸟瞰视图涉及的物理平面坐标系是路面，坐标原点是相机。

自我感悟

我想补充一点自己的感悟：

事实上，我觉得就算你得到了相机内外参，你想从ID上的某个像素点坐标计算出对应物理世界上的坐标根本算不出来！因为从物理3D世界上一个点到图像像素2D平面上一个点，必然会损失深度信息！比如你试着从$x_D$算出$x_B$，你算完$K^{-1}$和$D^{-1}$，你遇到$Z_c$，就算不动了，因为$Z_c$的值是从$x_B$得出来的，可是你要求的就是$x_B$啊！

你说，诶不对啊，我从畸变图像得到鸟瞰视图不就是得到世界坐标系吗！鸟瞰视图不就是反映了世界坐标系吗？不对不对，鸟瞰视图是一个2D平面，它反映的是物理世界平面，它自己就丢掉了一个维度的信息，你相机畸变图像也是丢掉了一个维度的信息，一样的，能转换。

所以，假如我们要根据一张相机拍出来的图像得到物理世界中两个物体之间的距离，我们该怎么算呢？好像我们也不能算出3D世界上任意两个点之间的距离诶，我们还是只能算物理2D平面上两个点之间的距离，例如，我们要算马路上一个路障到自身的距离。这就是“单目测量”问题，怎么算？我觉得跟鸟瞰视图是异曲同工的东西，你看你能用畸变图像生成鸟瞰视图了，也得到鸟瞰视图到物理平面的相似变换矩阵PBW了，那你岂不是得到物理平面上任意两个点之间的距离了，完成。