My Early Understanding of Basic Deep Learning Terminology

求导：

求导使用链式法则。下即标量对标量求导的链式法则： \[ y=f(u),\; u=g(x) \quad \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x} \]

trick：

想要加速训练，不用32位float而是16位float。
验证bug存在：对于分类模型，当output为未经softmax的评估分数时：未训练时，Hinge Loss应该=C-1，C是总类别数；无论在哪一个阶段，Hinge Loss最小为0。否则你的代码应该有bug。
验证bug存在：对于分类模型，当output为softmax后的概率是：未训练时，cross-entropy损失函数值应该是log(C)，C是总类别数。否则你的代码有bug。
如果损失函数曲线抖动很大的话，可以：1.降低学习率；2.增大批量大小(吴恩达有讲)。
CNN里，卷积层数越深(即便为了计算复杂度服务会把kernel做小一点)，输出通道数越多，往往模型越精准。
bacth_size不宜太过大，因为重复的样本会变多，影响训练数据的多样性，模型学到的都是些重复的没用的grad，这导致收敛变慢。举个极端的例子就是：训练集的样本全是同一张图片，你选batch_size为1学得的grad等同于batch_size为10，但要最终达到同样的acc，你后者要学的轮数是前者的10倍——所以这里我们说收敛速度，单位常常是epoch。若batch_size过大导致收敛变慢，如何解决？这时候可以提高lr，或者你运气好，数据集中类别本身就多，样本多样性丰富，那batch_size大一点也没关系。但理论上来说，batch_size变大会提高训练过程中的数值稳定性，而且batch_size过小也会降低收敛速度。
使用GPU要避免：频繁在CPU和GPU之间搬运数据；在GPU上有太多if-else等控制语句。
对权重w做更新，据说宜用w-=lrgrad，而非w=w-lrgrad，因为后者可能会导致requires_grad==False，因为后者求得w-lr*grad得到新值存于一个tensor中，再将此tensor值存入w中，从而丧失了requires_grad原有的值。但我觉得这样也说不通啊？
在train的过程中，越上层的w往往学得越快。
train过程中常用的一种手法是，lr随着epoch递减。这便要用到torch.optim.lr_scheduler.
看懂这样的操作：net=nn.Sequential() net.myfeature=nn.Linear(256,1000) net.myoutput=nn.Linear(1000,1)。其中.myfeature和.myoutput相当于是在net中添加的块的名字，名字是自定义的。
当模型是多变量预测时，尽量使得train set每个样本的label值足够分散(李沐课上那个案例是单样本的labels均值为0，方差较大)，这样更便于模型预测/收敛。我觉得其本质在于提高样本多样性。
提高分类/回归准确率的方法是TTA，即在测试时增广，使得net对增广出来的不同数据分别输出结果，多个结果取平均。其实，你还可以不在测试时对数据做增广，你可以训练多个不同的模型，对同一个输入数据输出多种结果，结果取平均即可。
学习率在训练时的变动不仅仅有cosine曲线之类的，你还可以在valid acc曲线趋于不变时把学习率往下调。
其实，有时候把valid acc刷太高也没有太多意义，因为这相当于把valid dataset也拿来训练了。
当一张图片很大时，若是想针对每一个像素都生成若干锚框，则计算开销太大，可以利用自编码器的思想，先用conv把图片的大小降一层，然后再生成锚框。也可以像yolo一样，不管你图片有多大，它都是按照一定的规则按h*w生成一些网格，而不是每个像素生成几个锚框，这样不论如何生成的网格/锚框都不会很多。
我们要微调在imagenet上训练的resnet模型，常常对输入的图片要做一个torchvision.transforms.Normalize处理，处理的参数是rgb_mean=torch.tensor([0.485,0.456,0.406])，rgb_std=torch.tensor([0.229,0.224,0.225])，这是resnet(pretrained=True)对输入图片的像素值(0-1之间)的硬性规定，因为resnet(pretrained=True)自己在训练时就对图片的像素做了这样的处理。但我听说现在pytorch上的resnet(pretrained=True)的输入好像也不需要这样的归一化了啊，不过做一下也没错。

求导：

深度学习里面我们用得最多的是对标量的求导。因为我们求导常常是对loss变量求导，loss变量是一个标量。假如loss变量是一个向量就麻烦了，想象一下一个向量的loss对一个向量x求导，得出一个2维张量，然后再对x求导，得到一个3维张量……以此类推，张量越来越大，还怎么算呢？

人类已知的全部求导方式大概分为3种：符号求导、数值求导、自动求导。

自动求导是深度学习中常用的求导方式。

自动求导要用到一种叫计算图的东西，可以说，计算图的存在就是为了方便自动求导的。准确来说，计算图更像是有一种便于你理解自动求导的工具——因为李沐说：“学习pytorch不需要深究计算图，但tensorflow要用到”。

计算图是什么？拿求导举例子，计算图相当于链式法则的图形化体现。其实我觉得，一个算式的计算图很像存储这个算式中缀表达式的二叉树。

计算图是如何构造的？有显式的构造(tensorflow/Theano/MXNet)和隐式的构造(PyTorch/MXNet)。前者对应符号式编程；后者对应命令式编程。前者是先构造出一个符号化的数学表达式，然后最后你要计算这个算式的话，就自己再输入变量，计算结果；后者是边构造数学表达式，边告诉计算机你此时键入的未知数符号的具体数值是什么，让计算机记住，当数学表达式构造完时，算式的结果也就被计算出来了。而在pytorch深度学习的计算中，我们常常使用隐式构造计算图而非显式构造，也就是说在做一个计算时，常用命令式编程。

(下面我们考虑的都是pytorch框架里用到的知识，在讲述深度学习时，指的也是pytorch框架下做的深度学习。毕竟李沐的全部课讲的就是pytorch。)

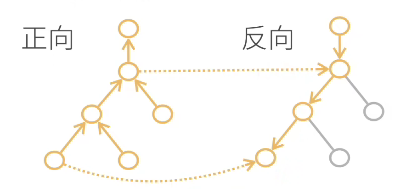
利用计算图，自动求导也可以分为两种模式：正向累积、反向累积/反向传递。

而在深度学习中，我们用的一般是反向累积/传递。

自动求导的两种模式

链式法则：\(\frac{\partial y}{\partial x}= \frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}} ... \frac{\partial u_2}{\partial u_1} \frac{\partial u_1}{\partial x}\)
正向累积：\(\frac{\partial y}{\partial x}= \frac{\partial y}{\partial u_n} (\frac{\partial u_n}{\partial u_{n-1}}( ... (\frac{\partial u_2}{\partial u_1} \frac{\partial u_1}{\partial x})))\)
反向累积、又称反向传递：\(\frac{\partial y}{\partial x}= (((\frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}}) ... )\frac{\partial u_2}{\partial u_1}) \frac{\partial u_1}{\partial x}\)

反向累积/传递：

反向累积是一种自动求导模式，y(x)对x求导，且y(x)的构造方法是隐式构造。反向累积的过程是什么？代码层面上先定义好x，再由x构造起y(x)——这也就相当于构造起了y(x)的计算图，此方式乃隐式构造。于是当你构造完y(x)时，你就拿到了一张y(x)的正向计算图，且由于是隐式构造，所以计算图构造的过程也是计算图被执行的过程，计算过程的中间和最终结果也被存储在了计算图中。接下来才是反向传递的正戏：你拿到了一张正向计算函数且存储了计算的中间和最终结果的计算图，然后你就可顺着这张计算图依照链式法则反向求导了。

(上面可以补充说明的一点是：你在代码上由x步步计算得到y的过程，pytorch框架会在背后隐式帮你构造起计算图，但假如你在写某段x参与运算的代码时不想要这段代码也被pytorch用来构造计算图怎么办？你给这段代码总体加上个“with torch.no_grad()”即可。如何理解“no_grad”？grad是求导得到的梯度，no_grad就是不求导，而计算图的构造就是为求导服务的，既然你不求导了，那我pytorch就不构造计算图了。)

反向累积/传递总结

构造计算图
前向：执行图，存储中间结果
反向：从相反方向执行图
- 去除不需要的枝

求导_1

Pytorch中，反向累积的函数是backward，用法是y(x).backward()。理论上来说，y(x)可以是自定义的任何函数，故而构造出来的y(x)的计算图不一定是一棵树，有可能是一个带环的图，具体视你这个函数的正向计算图而定。

但使用y(x).backward()函数有一个前提，就是在构造y(x)之前，你要事先激活x的gard成员变量，方法是x.requires_grad_(True)，等价于x=torch.arrange(4.0, requires_grad=True)#假设你想要个x=[0., 1., 2., 3.]。注意：x.grad被激活时初始值为NoneType。

激活x的grad成员变量有多个好处：1.李沐说的，grad存储最终y(x).forward()求出来的导数值；2.我猜的，给x激活grad变量让y(x,z)调用forward方法时，知道y是从x计算过来的，forward求导是对x求导而非z。y调用forward时怎么知道自己是由x计算过来的？貌似该信息被存储在y的成员变量grad_fn中。

Grad有个奇怪的特性：当你调用一次y(x).forward()求出对x导数存储在x.grad中时(y一般为标量，x为长度为n的一维张量，则求出来的grad也是长度为n的一维张量)，若是再调用一次forward，则x.grad中的旧值不会被清除，而是会留在那，跟这一次求导出来的是做累积，产生新值。Pytorch这样设计grad的目的在于：便于存储对loss连续求导产生的累积梯度。你要是像重置x.grad也行，调用x.zero_()即可——pytorch中的方法后带有“_”一般都是用于重写调用该方法的对象的内容。

优化算法：

优化算法，优化的是一个深度学习模型的参数，得到这些参数的最优值。

我们要训练出一个模型，模型的大概样子我们已经知道，例如是最简单的线性回归模型y=wTx，但这个模型里有很多未知参数，即为w=(w1, w2, w3, ……, wn)，我们训练模型，最终要得到的是w的最优值。

一开始，我们甩给计算机的是一个带有w随机初值的y=wTx，w的随机初值肯定不是我们最终想要的最优值，我们就要用一些方法来训练y=wTx模型，使得w中的某个wi越来越接近我们想要的最优值，这些方法就叫做模型的“优化方法”。

模型的优化方法里有一种最常见的，叫做“梯度下降法GD(Gradient Descent)”，它每次对所有样本的损失函数的加和求导，并迭代优化。它就要用到我们上面讲过的求导，求导是对y=wTx模型拟合实际数据的损失函数loss求导，grad=d(loss)/d(wi)。求导的结果用于不断更新wi的值，怎么用？wi=wi” – grad * n，n在此处被称为学习率，是一个超参数。

GD太贵了，我们对其做改进，每次只从全部样本中取一个固定大小的批量来求导，这叫做“批梯度下降法BGD(Batch Gradient Descent)”。

但是“bacth” GD算起来好贵，所以我们对它做改进，每次进来一个样本就求一次导，而不是对一批样本求导，你看一次求导变便宜了。这种叫做“随机梯度下降法SGD(Stochastic Gradient Descent)”。

但是BGD求一次导的bacth太大，而SGD求一次导只有一个样本，一轮epoch求导次数过多，所以我们二者取折衷，让BGD的每个批量的大小随着当前的求导情况而变化(怎么变化我也不知道)，得到“小批量随机梯度下降法MSGD(minibatch SGD)”。需要注意的是，若是采用小批量随机梯度下降法，则在优化模型参数的过程中可能需要逐渐减小lr的值，特别是当batch_size=1的极端情况，因为你的最终目的是得到一组模型参数使得所有样本的Loss最小，但你每次更新模型参数使用的仅仅是一个或几个样本，这可能使得你模型参数“下山的路径”并不是总朝着使得所有样本Loss最小的方向，看上去就是你的“下山路径”在震荡，特别是模型参数接近Loss最低点时，震荡最明显，总是无法收敛到最优解，你则需要降低你的lr了，以减小路径震荡，收敛到所有样本Loss最低点。

我认为，任何优化算法都有两要素：

模型的样子
训练所用超参数

以线性回归模型的训练举例子，线性回归模型实际上也就相当于单层神经网络，这个神经网络的参数包括权值w和阈值b。于是，对于线性回归模型来说，模型的样子可以有两种表示方法，传统的是y=xT*w+b，但我们也可以统一规范地用单层神经网络图来表示。训练所用超参数是学习率lr。

我们在实现一个实现某优化算法(例如SGD)的函数时，首先要明确这个函数的作用是不断根据损失函数对模型参数的梯度值来对模型参数进行更新。于是你要给这个函数传入的是梯度值(在pytorch中，用于w和b变量有数据成员grad，你只需要在优化算法函数外调用y.forward()，再往优化算法函数中传w和b即可)；于是这个函数需要实现知道优化算法两要素：模型的样子+训练用的超参数。

优化算法的实现还需要注意两点：

若是使用的SGD等需要用到梯度的算法，则每次对模型参数做完优化后，要对所有grad作一次清零
时常注意在对模型参数进行优化的过程中，不应当对已有计算图进行更新，不进行更新的方法有：
- with torch.no_grad():#回车
- detach()。 detach函数貌似是tensor变量存储的模型参数w、b的方法，但具体用法我忘了。

损失函数：

不论是训练/测试/验证集，数据都是以样本为基本单位的，而每个样本中会有多个指标和一个标签label，所以一个样本的数据就是用一个行向量+一个标量(对于训练集和测试集来说才有这个标量)来表示，这个标量就是标签label，在讨论训练出的模型的语境下，我们也叫它真实值。

在实际应用中，我们关注的主要不是损失函数的形式，也就是说我们工作的重心不在于损失函数如何通过output与target的计算出损失值，而是主要关注“损失函数值”，因为我们在反向传播对模型参数求导是，不是对损失函数本身调用backward，而是对loss(output, target)计算出来的值调用backward，才能计算出模型参数的grad。

损失函数值本身也可以看做一个以模型参数为自变量的函数，它具备三要素：

真实值
样本指标
模型参数。

也可以说：损失函数值由真实值和预测值构成。其中样本指标和模型参数共同运算出预测值，运算的法则即是模型本身。对于损失函数值而言，模型参数相当于自变量，真实值+样本指标相当于系数，故而损失函数值求导是对模型参数求导，不是对预测值求导。

理论上来说，仅仅采纳一个样本，用模型依据其指标的预测值和样本真实值的偏差也可以表示损失函数，但我们却往往不仅采纳一个样本，而是多个样本。理论上你训练模型的过程就是一轮轮不断更新模型参数的过程，每一轮更新采用的方法就是优化算法，例如SGD算法，每一轮更新你都要由损失函数对每个模型参数求导计算一组梯度，梯度的值往往用系数——即真实值+样本指标就能表示出来(eg线性回归模型)。而前面我们说过，求损失函数往往采用多个样本，你甚至可以使用训练集中的全部样本，但那样代价太高了，所以才有了“S”GD。

损失函数若是仅仅采纳一个样本，则预测值和真实值的偏差肯定是一个标量，因为真实值label本身是一个标量，而指标和模型参数运算出来的预测值也是一个标量。但若是损失函数采纳n个样本，则偏差的直接结果肯定是一个长度为n的向量，这时就要对这个向量做一定处理，例如对这个向量取范数值，得到损失函数最终的结果。

“损失函数”本身也可以表示预测值和真实值的“误差”，损失函数不同的形式则称作不同的误差，例如形如\(\frac{1}{2}\times (y-y^{'})^2\)称作MSE均方误差损失函数——但这个公式针对的是采纳单样本的损失函数，对于一般情况下采纳多样本的损失函数，y和y’有下标i，要做加和然后取平均，“取平均”，故而叫“均方”误差损失函数。

对均方误差损失函数还有一个改进：log_rmse，先对pred和label做log，再做rmse。

我们知道，sgd每次对param做更新时要原param-lrgrad，这里的grad是损失函数对param的导数，若是损失函数对批量样本的损失值仅仅是求加和而未取平均，则sgd公式适修改为param-lrgrad/batch_size。

分类问题中常用到的损失函数：

假如分类模型中输出的结果没有经过softmax变换，则可以直接对评估分数上Hinge Loss。对于Hinge Loss中为什么不正确分类的评估分数要+1，这是为了确保正确分类的评估分数远大于不正确的，事实上，你不一定要选用1，你可以选用其他数字。

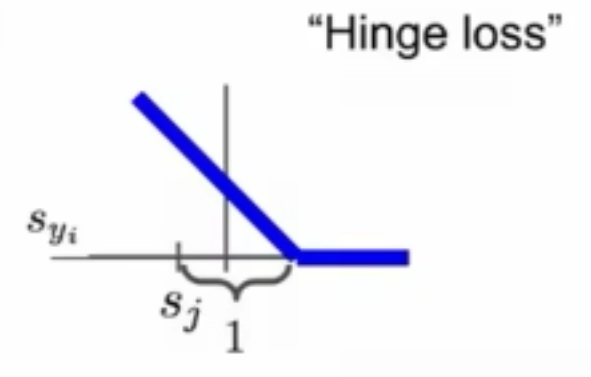
损失函数_1

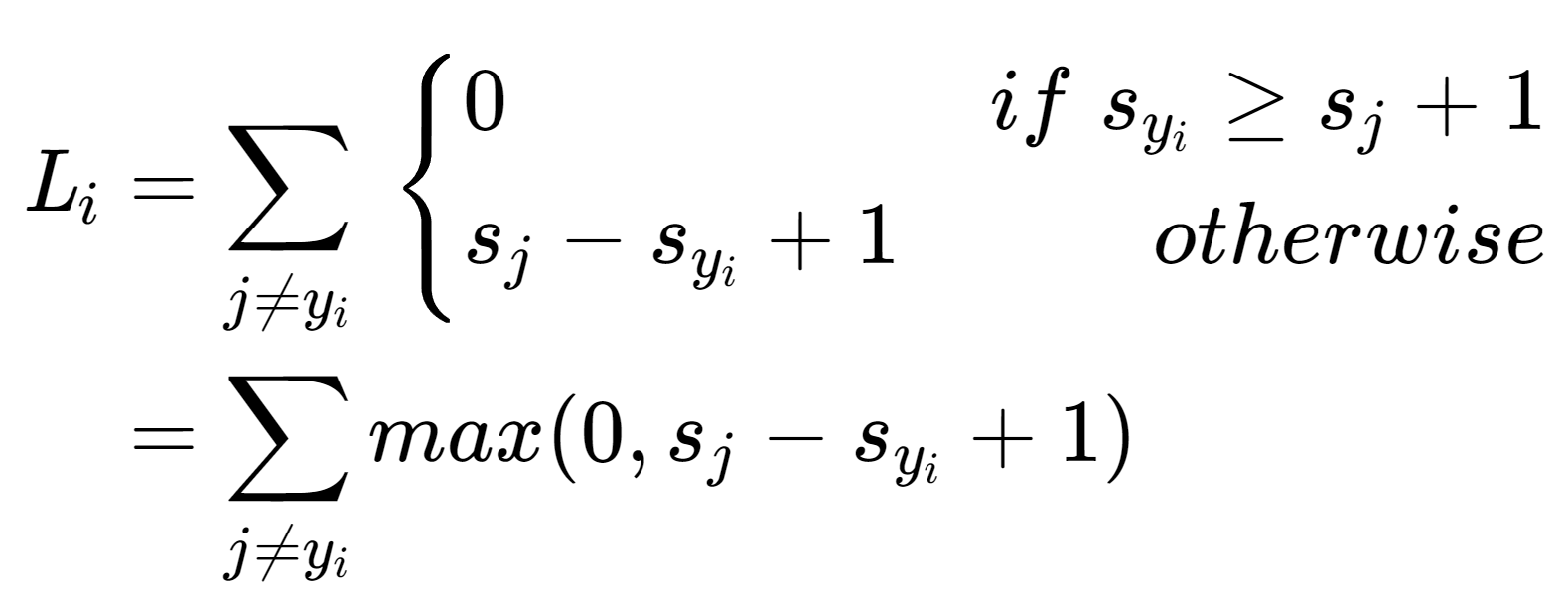
损失函数_2

Syi表示正确分类的评估分数，Si表示错误分类的评估分数。

假如你拿到的是结果softmax变换后得到的结果，可以用Cross-entropy Loss。

Softmax 模型

Softmax没有隐藏层。

Softmax回归模型虽然叫回归，但它其实是用于处理分类问题。

Softmax模型的input个数和output个数都不为1，softmax模型的结构本质上可以视作是多个线性回归模型的组合，有多少个线性回归模型，就有多少个output。

Softmax模型的输出是一个一维数组，每个元素是对相应分类的评估分数(也叫做置信度，只有分类问题才有置信度输出，回归问题是没有的)，而我们想得到的理想输出是每个分类的概率，如何将评估分数转换为概率？就要用到softmax函数，对每个output做一个变换——所以，实际上多个线性回归模型的简单叠加是不足以称为softmax模型的，还要在这些线性回归模型的output加一个softmax函数做变换，得到每种分类的概率，这才可以被称作softmax模型。

我们对softmax模型做训练，是要将它的输出结果尽量逼近[0,…1,…0]的形式，即是，若output有n个，则target的输出结果是一堆对应分类的概率，这些概率只有某一个为1，其他全为0。Output和target的损失函数我们一般用交叉熵。

这里我们可以看出来了，softmax模型是：线性回归模型的叠加+softmax变换，想要最终结果逼近target，损失函数一般用交叉熵，交叉熵函数的输入是softmax的结果和taget。但有时候，一些库(pytorch)提供的交叉熵损失函数的输入应当是线性回归模型叠加后直接输出的output，即是评估分数，交叉熵损失函数自动帮你对评估函数做softmax变换。

由于softmax变换的特殊性质，output变换后的结果永远无法得到理想的target，只能逼近。假如你想达到target的话，可以使用一个trick，不将target设为[0,…1,…0]，而是设为”Softlabel”，即是类似于[0.01, …0.9, …0.01]，这样output做softmax变化后绝对能直接完全等于softlabel，即为交叉熵损失函数为0。

关于交叉熵损失函数，我还想补充一些很有趣的信息论的知识。交叉熵损失函数其实源于信息论，你看交叉熵损失函数的形式是： \[ \textit{H}(p, q)=\sum_{i}-p_i log(q_i) \] 而信息论中，一条信息的信息量是-log(p)，p代表目标信息是正确的概率，比如说我说楚杰CV课不及格，那么这基本是不可能，它的概率p很小，信息量就很大。

引出另一个问题就是，log的底该是多少呢？我们取几都没关系，但我们约定俗成取2，因为取2后，算出来的结果可以以bit为单位，这样信息量就在实际应用中有意义了，一条信息的信息量=在通信中能用来表示这条信息的最短二进制位数。你想想是不是这个道理，一个硬币抛正面的概率为1/2，信息量=1，我们要表示这样一个结果，至少得用1bit的数据对吧。

那么，交叉熵损失函数与信息量的联系是什么呢？你看它是不是对于softmax模型输出的概率值的加权平均信息量！其中对于正确分类的权值大一点，错误分类的权值小一点，最终训练的效果就是让整个输出的信息量最小，而由于输出的概率值加和为1，所以为了达到这一点，正确分类的信息量会越来越小(输出概率值变大)，错误分类的信息量会越来越大(输出概率值变小)。

感知机：

多层感知机(MLP,multilayer perceptron)。

感知机是用来解决分类问题的，一般分为单层感知机和多层感知机。

单层感知机一般是单输出的，解决二分类问题。且只能解决线性可分问题，局限性较大。于是有了多层感知机，多层感知机可以解决二分类多分类问题，且能解决线性不可分问题，例如做异或运算(二分类，true和false)。

单层单输出感知机本身就是一个线性回归模型，靠激活函数才引入了非线性的部分，其他感知机以此类推。

对于常常出现的多输出的多层感知机，若是将其隐含层全部去掉，其将成为softmax模型。所以，按道理来说，softmax模型是一种特殊的单层多输出的感知机。而是事实上，多层多输出感知机输出的评估分数也要做一次softmax变换后才求交叉熵损失函数。当然，softmax变换nn.CrossEntropyLoss函数就已经帮你集成好了。

线性分类器：

这是对感知机的进一步理解：

用于分类的单层感知机即为线性分类器，它不会用到激活函数。线性分类器常用于图片分类，图片要输出，要先flatten成一维张量。
一般情况下，类别有多少个，线性分类器的输出就有多少个。但对于二分类而言，即有特殊情况，你可以有两个输出，但也可以仅有一个输出，也能实现二分类。
从“伪分隔面”角度理解线性分类器：对于一般情况下的多输出的线性分类器，其每一个输出都可以用output=wx+b表示，其中w是权重行向量，b是偏移值。而wx+b=0(位于该面上的样本output均为0)可以视作n维样本空间(n维取决于线性分类器有多少个输入)的n-1维“伪分隔面”，为什么叫做“伪分隔面”？因为它不是“真分隔面”，它并没有真正实现该n-1维分隔面将其分隔的一边的样本严格划分为一类，另一边划分为别的一种或多种类。每一个output对应一个伪分隔面，每一个伪分隔面让其一边越远的样本更有可能隶属于该分隔面对应的分类，另一边越远的样本更有可能隶属于其他类，只是“有可能”，而非绝对划分，所以最终的分类结果还要看每一个output的评估分数比较相对大小。而其实，上面说的都是多输出多分类的一般情况，还有用单输出实现二分类的特殊情况，在这种情况下，伪分隔面就能完全实现wx+b=0严格划分n维样本空间为两类，因为一边的样本wx+b>0，另一边<0——这里值得注意的是，不同的权重w可能在n维空间中作出同一个伪分隔面wx+b=0，但同一个伪分隔面的一边的样本，对于不同的权重w可能是wx+b>0，也可能是w*x+b，所以一组权重可以唯一确定一个伪分隔面，一个伪分隔面不可以唯一确定一组权重。
从“模式匹配”角度理解线性分类器： W*x+b=OUTPUT，W的每一个行向量对应于一个output，即对应于一个分类。要让某类的图片被成功分到i类，则相较于其他类的行向量，该类的行向量w应当与input最为相近，也就是说，某类对应的w是某类图片的一个“模式匹配”。我们将w行向量reshape(size(原图片))，一定会发现w在reshape后形成的图片与该类别的图像有相似之处。
线性分类器无法实现在n维空间中的非线性分隔(例如异或运算。分类问题是离散问题，所以异或运算是分类问题而非回归问题)。
在线性分类器利用权重行向量w给图片特征打出评估分数之前，我们常常做这一步操作：对图片像素做一定转换，提取出特征向量，输入线性分类器，而非直接用图片原像素作为特征向量。为什么要这么做？有两个角度的理解。角度一：模式匹配。线性分类器的输入若直接是图片像素，则对应类别的权重行向量w是对该类图片的一个模式匹配，但这种情况无法处理多模态，例如“马”类的图片，马头可能朝左，可能朝右，这就是二模态，w做reshape产生的模式匹配图像看上去就像是有两个头的马，这会降低线性分类器的精度。于是我们对图像原像素做一定转换，让多模态的某类图像们通通变成单模态，这样w就只用兼顾这一种模态就可以了。角度二：单层线性分类器无法处理复杂分类。一个特征空间中有两类样本，但要划分开这两类样本需要用到非线性的真分隔面，于是单层线性分类器无法处理它。于是我们不使用原特征空间的特征，而是对样本的特征做转化，成为一组新的特征，在新特征空间中的两类样本能够被线性分类器划分开。这既是将不可分的样本线性可分化。

激活函数：

激活函数的本质在于引入非线性性。

对输出层往往不需要添加激活函数。

训练/验证/测试数据集：

在训练集上的误差是训练误差，在验证集上的误差是泛化误差。我们关注的是泛化误差。

训练数据集是用来训练模型参数的；验证数据集是用来验证训练的结果，查看训练过程中设置的超参数训练模型的效果，几次训练下来，通过模型在验证数据集上表现效果的对比，来选取合适的超参数——验证数据集是用来选择超参数的；测试数据集一般用得很少，它相当于最后的高考，训练数据集相当于平时做的练习题，验证数据集相当于模拟考试，我们千万不要把测试数据集和验证数据集混用。

一般给你一个数据集，你要将其划分为训练数据集和验证数据集，如何划分出验证数据集？当你的总数据集过小时，划分出验证数据集的比例太高是一种浪费，我们最好将更大部分的数据集划分出来作为训练集，所以我们常常使用一种K则交叉验证的方式，即是将整个数据集划分为k端，每次将第i段数据用来做验证集，将剩下的k-1段数据用来做训练集，将最终一共k段验证集验证得出的loss或accuracy的平均结果作为验证集的验证效果。K则交叉验证让你最大程度地利用了总数据集的更大部分来训练。其实还有一种更极端的情况，就是假设总数据集共有n个数据，你采用n则交叉验证，这样最大长度利用了数据集，但算起来太贵了，因为你要训练+验证n/1=n轮。

当总数据集足够大时，我们也用不着做k则交叉验证。

正则项：

模型容量本意是拟合一个函数的能力，也常用以描述一个模型的复杂程度。

在统计学习知识范畴内，有一个VC维的概念，它一般用来描述一个分类模型的容量，一个分类模型的VC维为：对于容量小于等于n的数据集，给该数据集中的样本任意标label，该模型都能完成其分类，则称该模型的VC维为n。

对于一般的神经网络模型，我们衡量模型容量往往不是用VC维，太难了，而是参考的两个指标：权值w(和偏移b)的数量和取值范围。对于简单的数据集而言，我们训练的神经网络不宜过复杂，否则容易出现过拟合。限制模型复杂度的角度也就是w的数量和取值范围，w的数量你根据神经网络的层数和宽度即可限定，而w的取值范围就能牵扯出一个“权重衰退”的知识。

首先我们要明白，为什么权重的数量和取值范围会影响模型的容量，权重的数量好理解，那取值范围又是为什么呢？假如权重的取值范围过大的话，则神经网络可以拟合出一个不平滑且复杂的曲线，反之拟合出来的曲线一般都很平滑。

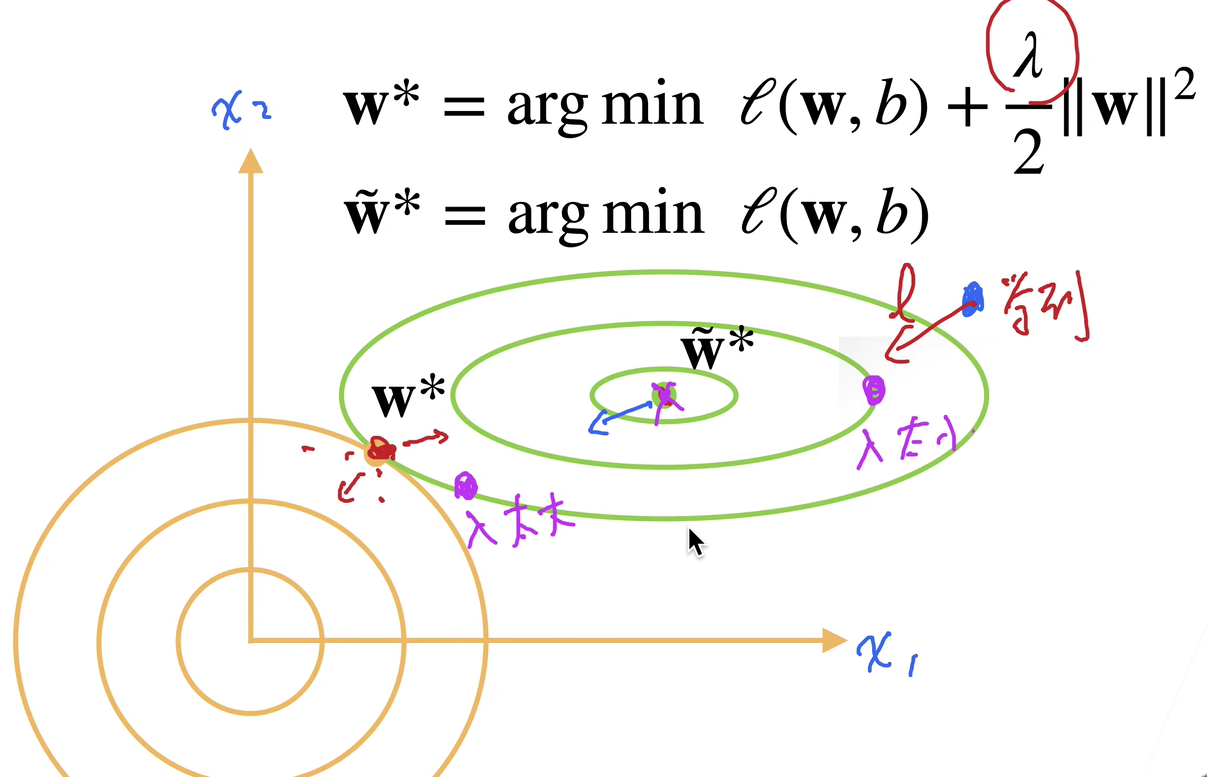
如何限制w(模型参数)的取值范围？写成数学表达式，有两种写法，一种叫“刚性限制”： \[ min\; \textit{l}(w,b)\quad subject\; to\; \left\Vert w \right\Vert^2 \leq \theta \] 一种叫“软性限制”： \[ min\; \textit{l}(w,b) + \frac{\lambda}{2}\left\Vert w \right\Vert^2 \] 其中拉姆达是个正数，拉姆达越大，对w的限制越大，当拉姆达==0时，对w没有限制。

软性限制的形式更容易被我们的机器学习训练过程所体现，所以我们一般也采用软性限制的写法来描述模型参数的取值范围限定。体现在机器学习训练过程中，我们相当于将软性限制整个作为一个新的损失函数，其中的lambda/2*||w||^2又被称作“惩罚函数”。当采用SGD来优化模型参数时，更新参数的表达式变成了： \[ w_{t+1}=(1-\eta\lambda)w_t - \eta \frac{\partial{\textit{l}(w_t,b_t)}}{\partial{w_t}} \] 你可以看到正规的SGD模型参数更新公式里wt的系数为1，这里却乘了个小于1的系数，所以我们叫上述限制模型参数取值范围的方法为“权重衰退”。但在实际的训练机器学习模型的过程中，我们实现权重衰退的方法一般不是改动损失函数成软性限制的形式，因为这会让自动求导变贵，我们一般是给SGD优化器一个weight_decay参数，即是lambda，直接给wt乘系数，便宜一点。

要注意的是：我们管\(\Vert w\Vert\)叫L2范数，其标准写法应该是\(\Vert w\Vert_{2}\)。那这里L2范数作为损失函数的一个项，我们为什么叫它L2“正则项”呢？其实，在损失函数中任何项，只要它起到的作用是防止w取值范围过大，我们都叫它正则项。推而广之，若是一种手法能使得模型参数w取值范围不过大，以起到防止过拟合的作用，我们就称这种手法为一个正则，例如权重衰退就是一种“正则”。其实这里的正则项，不一定要用L2，也可以用L1，只是L1对模型容量的衡量是W矩阵有多稀疏(0元素的多少)，L2则更关注W所有元素的整体分布。这里还有一个trick，如果你只想限制W中某几个参数的大小，也可以针对这几个参数制定惩罚项。

其实，模型训练产生过拟合的根本原因在于训练样本中存在噪音(噪音可能导致模型学习到错误的信息，从而影响模型在未见过的数据上的泛化能力)，这些噪音会导致训练出来的模型参数w过大(绝对是过大，而非过小或别的什么，这个可以数学证明)，即是离最优解w变远，所以需要给损失函数加上一个L2正则项将训练出来的模型参数w往小了拉(权重衰退)。但假如你的训练样本中没有噪音，那你训练出来的模型参数w将不会受到干扰，训练出来的模型参数只会倾向于逼近最优解，这个时候就不需要权重衰退了。也就是说：样本噪音是导致过拟合的根本原因，有噪音的训练集越小+模型容量越大\(\to\)过拟合越严重，权重衰退本质上就是解决样本噪音导致的过拟合问题。

正则项_1

限制模型容量以防止过拟合的方法除了权重衰退之外，还有dropout，也叫丢弃法。不同的是，dropout的参数更直观好调，但只能应用于全连接层，但权重衰退应用范围却更加广泛。

有一种防止过拟合的思路叫做Tikhonov正则，基本思路是训练模型时在数据样本中加入随机噪音(其实我不知道这里的加入噪音是在一大堆样本中有几个样本是噪音，还是一个样本中有几个特征是噪音)，使模型具备良好的鲁棒性，也能起到限制模型容量的效果(达成的效果相当于限制模型参数取值范围)。Dropout正则就是一种常用的实现Tikhonov正则的方法。但dropout和Tikhonov原意的不同点是：dropout正则是在神经网络的隐藏层(仅限于全连接层)的输出加入噪音，而非是在输入层的样本中加入噪音。Dropout正则要遵守一个原则是：一层神经网络输出的数据在加入噪音后，这些数据的期望值不会改变，也就是E(x’)=x，其中x’是加入噪音后的输出数据。

Hinton在提出dropout方法时，本意是在训练过程中dropout正则每轮batch能将整个神经网络划分为多个子网络，对这些子网络分别进行训练，最终平均得到的总神经网络模型效果会更好。为什么说是划分为多个子网络？因为dropout方法将隐藏层中的某些神经元的输出设为了0，那么loss对对应wi(某个神经元输出所连接的wi可能有多个)求导得到的结果为0，按照SGD优化算法，对应神经元输出连接的wi就不会被更新，所以相当于该神经元输出所连接到的wi没有被训练，相当于缺失了这个神经元，于是dropout从总神经网络中删除了一部分，留下的就是子神经网络(子神经网络神经元输出的结果被做了简单的乘法加法数值运算，以使得输出值的期望跟未dropout的一样)。但是后来的人研究dropout方法时发现，与其说dropout达到了hinton想要的目的，不如说dropout起到了：通过在模型训练过程中加入噪音，限制模型参数取值范围从而避免过拟合的作用。所以dropout应该是一种正则，一种Tikhonov正则。

用pytorch实现dropout可以在神经网络中加入nn.Dropout层。我记得是：dropout层只在训练时起作用。所以，在训练net时，你要用net.train()语句，在推理时，你只需要用net.eval()就能注销掉dropout层了。

有一个很能反映Tikhonov正则思想的正则项，叫做“数据增广”，其中对图像数据进行增广的方法在torchvision.transforms里有提供。图片数据增广里有一个很奇怪的增广叫mix-up增广(好像也叫跨图片增广)，它不仅要将两张图片的像素进行叠加，还要将相应label进行叠加——而除了将像素进行叠加，还可以把两张图片拼成一张图片，同时label也加权求和。

数值稳定性：

数值稳定性在神经网络训练过程中表现为模型训练时不会因为输入数据的微小扰动而性能大幅震荡，甚至无法收敛。

事实上，数值不稳定的原因中，梯度清零的情况多于梯度爆炸。

不一定参数多，或者层数深的模型数值就越不稳定，因为若是一个模型层数较深，但它每一层运算的output值都不大不小，然后运算的时候一层一层累积起来也是靠的加法而非乘法(虽然我也不知道靠加法如何累积其层来)，那么它也是不一定会出现严重的梯度爆炸或消失的。

一个模型要保持“数值稳定性”，体现在两个方面(主要是前者)：

训练过程中不要出现梯度消失(导致w更新速度过慢)或梯度爆炸(导致产生inf或nan)，也就是说梯度维持在一定范围
模型每一层的输出值不要过大或过小，维持在一定范围(事实上我认为这一点也是为了满足第1点，每一层output范围合适，求导结果也能缓解梯度爆炸/消失。想想对(WX)^2求导)(后来我才学习到，原来要是每一层的输出值太大了，也可能会导致16/32bit浮点数溢出，模型完蛋)。

其中最重要的是第1点。

说具体点：正向角度看，我们希望每一层的输出h期望都为0，方差都相等；反向角度看，我们希望Loss对每一层的输出h(为什么不是权重w？因为数学推导出来是这样。其实都一样。)的导数期望都为0，方差都相等。

而上述两个方面的要求我们都无法完全满足任意其一，我们所做的一切都只是缓解，或者说，尽量防止数值不稳定。我们如何缓解数值不稳定？可以从模型参数初始化和超参数设置(激活函数)两个角度入手。

经过数学推导(具体过程不提及)，尽量满足数值稳定性，我们需要：

模型参数w(视作随机变量)初始化时，每个参数的期望应当为0
模型参数w初始化时，每个参数的方差应当满足上一层的宽度这一层的方差=1，以及这一层的宽度这一层的方差=1
激活函数在x=0附近应当尽量接近于y=x。

上述3个条件中的第一个很好满足。

第二个条件的两个子条件难以同时满足，怎么办？我们采用“Xavier初始”，即是我们折中一下，将两个子条件合并为“这一层的方差=2/(上一层宽度+这一层宽度)”。

第3个条件要满足，根据泰勒展开，我们选用tanh或relu激活函数皆可，sigmoid不太合适，除非你对它做一点变换：f=4*sigmoid-2。

有一个疑问在这里：反向来看，为了维持grad不消失/爆炸，我们让dLoss/dh维持在一个小范围内，这是不得已而为之，可以理解。但为什么要求正向来看(每一层)输出h也维持在一个小范围内？不怕损失模型的表达能力吗？其实不怕，因为模型的最终输出值在什么范围都无所谓，关键是要看你如何描述这个输出值，比如输出的像素值在0~1，你可以描述为0~255的像素值。

问题：为什么要把w初始化时期望设为0？不能是其他值吗？我也不知道，数学推导时，有个假设前提，假设的就是w初始化时期望为0。而且我怀疑，w初始化期望为0，方差符合Xavier初始，激活函数也满足要求，能保证数值稳定性——但在后面对w更新的过程中，w的期望和方差还能不能维持初始化的状态？假如不能，岂不是不能保证输出稳定性了？我想这也行就是为什么说我们所做的只是尽量保持数值稳定性，缓解数值不稳定吧。

防止梯度爆炸还可以在一个地方做优化，即是使得输入数据不至于太大(取log，减mean()等)，然后学习率不能太大，虽然我觉得这种优化是治标不治本。

处理在模型参数初始化和超参数设置等角度缓解数值不稳定外，还可以用梯度剪裁、批量归一化等手段缓解数值不稳定。

在深度学习中，遇到的最多的数值不稳定的问题是梯度消失，而解决梯度消失的根本性方法是residual connection，其源于ResNet。其防止梯度消失的方法可概括为深层梯度的计算“乘法变加法”。

梯度剪裁：

梯度剪裁很简单，梯度剪裁专攻梯度爆炸。

梯度剪裁就是将模型训练时反向传播求导得出的每个模型参数的梯度拉成一条向量，然后你求这个向量的L2范数，看它是否大于theta，小于就不管，大于就让它的L2范数压成theta，theta值是你认为设定的。

批量归一化：

Batch Normalization，normalization一般翻译成归一化，有别于regularization的正则化。

BN一开始提出来是为了：

解决梯度清零，提高收敛速度
但它也附带了正则化的功用。

BN常置于conv或linear后面，激活函数或pooling前面。

前面我们讲过从模型参数初始化和超参数设置角度保持数值稳定性的3大条件，但它们是从模型参数初始化入手缓解梯度爆炸和梯度清零的。这里的BN是专攻梯度清零的，且它的解决方案不是针对模型参数，而是针对每一层的输出数据X，它相当于给神经网络新加了一种层，让X符合一种归一化/标准化分布，从而使得模型深层的grad和浅层大小相当，缓解梯度清零——具体怎么样的分布为什么能缓解梯度清零？这是数学上的问题，我们先不讨论，会用就行。需要注意的是，这里的BN层也有需要学习的参数，所以BN层不仅仅在训练时发挥作用。

BN是如何通过缓解梯度清零来实现提高收敛速度的？梯度清零带来一个问题：靠近输出层的grad比较大，靠近输入层的grad太小，于是lrgrad导致浅层w收敛快，深层grad收敛慢(有一个很有意思的点，浅层的w很快就学习完了，但等到深层的w慢悠悠稍微改变了一点点，浅层w又得全部重新学习了)，而决定一个舰队航行速度是最最慢的那艘船，于是模型收敛速度慢了。同时，你也不能通过提高lr来提高收敛速度，因为lr大了，浅层受不了，lr小了，深层受不了。于是你用了BN，BN让浅层和深层的grad大小基本均衡，深层gradlr变大了；同时你可以放心地提高学习率，不用担心grad过大导致浅层受不了了——于是收敛速度变快了。

BN是如何附带了正则化的功能？还记得Tikhonov正则化吗？BN相当于给模型的每层输出X加入噪音，从而像dropout一样实现了Tikhonov正则化。但要注意的是，BN和dropout不能混用，否则模型效果很不好，这是前人通过实验得出的。

对BN公式的理解，看不看都行：BN按道理来说，只用将每层输出的X减均值除方差实现归一化即可，为什么还要给已经实现归一化的结果做一次线性变换呢？(线性变换的两个系数即是BN层需要学习的参数)这是因为单单X减均值除方差的话，X的期望就是0了，而对于很多激活函数而言，其在0点近似于y=x，这样激活函数的作用基本没有了，它没有引入非线性性，为了防止这种现象，对已经归一化的X在做一次线性变换，使其期望不为0，照顾激活函数。实际使用时，torch.nn里有现成的BN层，BatchNorm1d用于全连接层的一维输出，BatchNorm2d用于卷积层的2维输出。

在学习BN的过程中，发现了一个很有意思也很重要的点：神经网络中，不论是全连接层还是卷积层，输入输出的张量至少是2维，而且，第一维必定是批量维(代表样本个数)，第二维必定为特征维。对于卷积层(4d)来说，第二维还是通道维，卷积层的输入一个样本，有多少个通道表示该样本有多少个特征。顺着来，还有一个很有意思的点：kernel=1x1的卷积层相当于一个全连接层，对于这个全连接层而言，若一次输入一个样本，该样本有n个channel，每个channel有m个像素，且输出有p个channel，则相当于给全连接层的的输入有m个样本，每个样本n个特征——本来对于卷积层而言，应该是1个样本，n个特征的。