Deep Learning (CV)
Mainly CNN
KNN(k-Nearest Neighbors):
K最近邻算法,它是一种有监督的机器学习分类算法,和无监督的k-means有着本质区别。
KNN是一种对图片进行分类(classfication)的最笨方法。 KNN有一个超参数k,那k==1的情况举例子:训练时,你的模型先记住训练集中的每个样本;预测时,传入测试样例,找到训练集中和测试样例最接近的一个图片,该图片所属target即是测试样例所属target。当k>1时,就是找到训练集中和测试样例最接近的k个样本,这k个样本可能属于不同的target,使用这k个样本离测试样例的距离+属于不同target的样本的数量+一些权重做变换,最终得到测试样例应属的target。你可以理解的是,K值选取的越大,KNN模型对噪音的鲁棒性就越好。
KNN还有一个超参数,什么方法判断两张图片的接近程度?最常用的是两张每个像素之间作差得到一个张量,而后,或求L1范数,即是两个张量的曼哈顿距离;或求L2范数,即是两个张量的欧氏距离。大多数情况我们都是用L2范数/欧氏距离,那什么时候用L1范数/曼哈顿距离?由于同样两个样本点的曼哈顿距离在不同的坐标系下值不同(欧氏距离则没有这个问题),所以曼哈顿距离有“坐标系依赖”,故而当两个样本点的各个特征有特殊重要含义时,宜用曼哈顿距离;当两个样本点只是某个空间中的一个通用向量时,或者你不知道那些特征的具体含义时,宜用欧氏距离。
KNN为什么在图像分类中没有得到广泛应用?有3个缺点:
- train时间复杂度过低,predict时间复杂度过高
- 接近程度的比较方法不论是L1还是L2都有失偏颇
- 想要KNN算法对图像分类足够精确,则训练集中的样本在空间中的分布应该足够密集。而空间的维数越高,则覆盖一定尺度空间所需的样本就越多。对于图像而言,每个像素点相当于某个维度上的特征,那图像样本所属的空间是一个超高维空间,想让KNN分类足够准确,所需的样本太多了,predict时间复杂度O(n)太贵了。
卷积层:
下面说的卷积层都是二维卷积层,二维卷积又称作二维相关操作。
卷积层时怎么来的?卷积层是由全连接层推导来的,它本身是一个特殊的全连接层(这个全连接层的权重大多数都是0)。我们希望有这样一个全连接层,它能提取出一个图片的特征。
提取出一个图片的特征,这个提取器必须遵守两个原则:
- 平移不变性
- 局部性。对于全连接层来说,这个提取器就是层的权重。
对于输入是一个矩阵,输出也是一个矩阵的全连接层来说,其权重张量是4维的,好理解。
于是,我们先让这个权重张量遵守局部性,于是对于输出的神经元,我们只需要输入矩阵中某一小块的数值,这便使得权重张量产生了大量的0,虽然非0部分大小和值不一定相等;然后让这个权重张量遵守平移不变性,于是对于输出的每个元素而言,其对应的权重张量非0部分的大小和值是一样的,便唯一确立了卷积核。
上面的特殊全连接层是卷积层,那卷积核是什么?是输入输出都是矩阵的全连接层的每个输出神经元对应的权重张量的非0部分。本质上,全连接层的权重张量是4维的,但只考虑卷积核,我们常说该卷积层的输入输出和卷积核都是二维的,我们做的是二维卷积。
其实严格来说,我们用的应该叫做二维交叉相关,但由于不考虑数学上的表示,在实际使用过程中,二维卷积和二维交叉相关是一样的,所以我们直接叫二维卷积了。
卷积核的大小我们又称感受野。
卷积层有两个超参数,padding缓解减少量,stride倍增减少量。
卷积输出的结果叫做输入的feature map。
卷积层卷积一次输出一个像素值,该像素值的计算也可以有偏移量bias,一般是有的,你可以给pytorch的conv函数传bias=False让它没有。
卷积层等价于一个受限的全连接层(kernel=1x1相当于一个全连接层了,常用于改变输出通道数而不改变feature map大小,要改变也可以,stride变一变),相比于全连接层它的模型容量要小很多,所以过拟合现象不那么严重。
设计一个CNN时,往往卷积核的大小越大,卷积层数越浅,这是为了计算复杂度服务,不然卷积层数也做多了,计算太贵,而且也容易过拟合。有时候一个kernel size太大了,我们不仅要降低模型深度,还要减少输入输出的channel数。
一个CNN,每层conv在提取特征输出feature map,越下层的feature map每个像素提取到的特征越局部,越上层则越整体;越下层的feature map越还原图像的原貌,越上层的feature map越抽象。
有些CNN在某些情况下对输入图片的大小有要求,这些CNN可能具备以下特点:
- CNN每个stage使得feature map的size减半,假如input的size太小,可能使得未达到预定深度时,feature map的size就小得无法减半了
- CNN最后部分有flatten操作,然后接全连接层,全连接层的input有数量要求,假如输入图片的size不对,则feature map到达flatten后,得到的一维向量的size可能就不符合全连接层的input要求
- ……
池化层:
卷积层对输入图片各特征的位置十分敏感,例如同一张图片,你稍微让它左移一个像素,那后序的神经网络可能就认为卷积层提取出来的特征就完全不一样了。
为了缓解这种现象,我们引入了池化层,相当于对提取出来的特征做一下模糊,让卷积层对图片各特征的位置不那么细致入微地敏感,提高模型的泛化能力。
其实,池化层还有一个作用是将feature map的size变小,减少计算量。
Torch.nn默认的池化层函数的stride等于池化核的大小。
但现在池化层用得很少,主要有两个操作淡化了池化层降低卷积层敏感性的功能:
- 池化层的操作可以被卷积层学出来
- 输入模型的样本本身做了很多旋转,平移等操作,卷积层能看到不同位置的特征,也就不会认为两个特征位置稍微不同的图片特征不同了。
我认为,降低卷积层对特征位置的敏感度,是不是等效于防止过拟合?
经典卷积神经网络:
CNN的设计从VGG开始引入了“块”的设计思想,VGG、NiN等都是设计CNN的思想。
我们描述一个CNN的结构,常以stage为单位,feature map的size每减少一半,就是一个stage。而且,我们在设计时,常常feature map size减少一半,channel数就增加一倍,这是为什么呢?因为卷积往往会使得feature map的size不断减小,虽然是在summarize information,但终究会导致信息的丢失,不过我们要是使得channel变多,则虽然一张feature map蕴含的信息随着size变小了,但是feature map却变多了呀,保留了很多信息。
- LeNet
- AlexNet
- VGG VGG更像是一种架构CNN的思想,它是对AlexNet的改进,它的基本构造单元是若干VGG块+3个全连接层。全连接层有特定的模样,它和AlexNet最后的3个全连接层一样。VGG块也有特定的构造细节,对于一个VGG块来说,它的超参数只有其每个卷积层的通道数和卷积层的层数。VGG网络的写法常有:VGG-16、VGG-19……后面的数字表示该VGG网络中含可训练参数的层数,也就是说,池化层、dropout层和激活函数层不算。
- NiN 基于VGG改进,从此,去除了CNN末端的全连接层。NiN有属于自己的NiN块,但它将最后的全连接层取缔,改为一个全局池化层,池化得到的结果即为评估分数。去掉了强大的学习能力强的全局池化层,虽然减缓了模型收敛的速度,但却缓解了过拟合,提高了模型的泛化能力与预测精度。
- GoogLeNet inception块。Inception块相比于同样层数的3x3或5x5卷积,模型容量都要小,你看,它有很多层都是1x1的卷积层专门用来降低通道数,从而降低模型容量——这样做的目的也是为了减少后面3x3或5x5卷积的计算负担。
- ResNet 残差(residual)块。残差块的residual connection使得真正的“深度”学习成为了可能,能有效防止深度学习中常见的梯度消失。
并行计算实现高性能:
在训练过程中,用并行计算实现高性能,往往会被卡在设备通讯的瓶颈上(包括读取内存)。并行计算中,计算/通讯比越高,计算的性能就越高。计算即为FLOPS,通讯可以理解成每做一次flo,要从其他设备那里读取多少bit数据(实际上,通讯时间的影响因素还有带宽)。我也不知道为什么,通讯的耗费可以等效为模型的大小,模型越小,通讯耗费越少,越适合做并行计算,例如模型容量:inception < ResNet < Alexnet。
多GPU训练:
为了将一批量的数据拆分,torch.nn提供nn.parallel库里的scatter函数,但只有在手动实现多GPU训练时你才会用到这个库手动拆分数据。
手动实现多GPU训练是很困难的事情,若要直接调包则很简单,直接将net通过nn.DataParallel复制到不同GPU上就行,在用net(X)时,net即会自动帮你拆分X并多GPU运算。
我们实现多GPU训练时,看模型训练的速度,衡量标准往往是多久训练完1epoch,若是你发现多GPU的速度不比但GPU快多少时,原因往往有:
- 计算量本身就小,没把GPU的core调动起来
- 大部分时间花在了内存访问而非数值计算上……处理方法往往是,提高batch_size的大小,但batch_size越大,收敛速度越慢,看你如何权衡了。
分布式训练:
这和多GPU训练其实没有本质区别。
进行分布式训练要注意的一些点是:尽量避免时间浪费在设备时间的通讯上,如同多GPU训练中让数值计算次数多于内存访问次数一样。如何做到?可以提高batch_size,尽量使得数值计算的时间大于设备通讯的时间,且较好地调动GPU的多核。
微调:
微调是迁移学习领域的一种算法。
这里我们先只讨论分类器的微调,我们要先了解分类器的本质:任何分类器都可以视作两部分:最后的线性分类器(+softmax),以及前面的所有特征提取层。特征提取层将输入数据的所有特征提取到一个线性可分的语义空间上来,然后在该语义空间上做线性划分。但在有些CNN(例如NiN)里也可能干脆隐去线性分类器,因为最后只是一个池化层来提取最后的特征,池化完也就分类完了——但你要知道分类器的本质在于将特征提取到线性可分的语义空间中。
由上述可以知道,对于一个CNN分类器而言,越深的layer越通用(低层次的特征),越浅的layer参数越专有化(特定数据集相关特征)。
微调的通用做法是,我们拿到一个pretrained的模型,将其原本线性分类器换成一个新的,然后在目标数据集上对“旧特征提取层+新线性分类器”做训练。我们可以在此基础上改进,下面几种方法是步步递进的关系:
- 整体的学习率改小,这是一种正则项。因为原模型已经pretrained了,特征提取层已经很成熟了
- 线性分类器的学习率调大,比特征提取层大得多,因为新的线性分类器权重要重新训练要它更快点。虽然根据数值稳定性部分的知识,线性分类器的grad本身应该比特征提取层的大
- 把较深的layer的w固定不动,不train了
- 若是原数据集的label有一部分与新数据集重合的话,可以选择不完全删去原模型线性分类器的w,可以保留重合label分类对应的w,置于新模型中
- 在一些极端的情况下,若是就数据集的label完全包含新数据集的label,则可以直接在旧模型的输出层加上一个线性分类器,旧模型的参数不变(param.requires_grad=False for param in net.parameters()即可),只训练新线性分类器的参数。
微调带来的好处是:更少的epoch与时间可以带来更高的模型精度。
锚框用于目标检测:
一般的流程为:
- 导入一张图片(图片本身有真实框的labels,每个真实框有标号,标号往往对应着某种类别,狗或猫),按照某个锚框生成算法生成大量锚框,每个锚框为一个训练样本。锚框生成算法我们假设用最简单的,就是每个锚框生成一组由参数size和ratio决定的不同大小的锚框,s和r怎么确定呢?一种方法是随机确定,一种方法是统计图像中groud truth/bounding box的大小,然后依照这些bounding box的大小来生成决定s和r,为什么这样做?因为万一你要检测的物体是电线杆,那么你这个s和r的参数会选得很极端,你怎么知道s和r的理想选取值会怎么极端啊?
- 由每个锚框与每个真实框的IOU值,根据某个前景框筛选算法选出部分锚框作为前景框,分别和某一个真实框的标号相对应。一般我们针对一个真实框,你可以选出多个前景框来跟它对应,用以训练(反正模型推理得到了该真实框的多个bouding box,你还要做nms筛选);
- 根据某个偏移量算法计算出每个前景框到对应真实框的偏移值;
- 一张图片的每个锚框为一个训练样本,上述过程你已经打好了每个训练样本的锚框信息,锚框信息=(1.该锚框(1)是否与(2)哪一个真实框标号匹配?2.该锚框到对应真实框的偏移值?);
- 你可以拿打好的样本的锚框信息去训练模型了;
- 模型做预测。模型不是直接预测和真实框相匹配的预测框,而是预测出每个锚框的锚框信息。后面还要通过一定手法根据这些锚框的锚框信息前景框候选预测框预测框。照样导入一张图片,图片按锚框生成算法生成大量锚框,每个锚框即样本,模型对每个锚框预测出label。根据label,从这些锚框中挑出前景框,再根据偏移量算法将前景框换算成候选预测框。每个真实框标号对应多个候选预测框,你下面还要对每个真实框标号对应的多个候选预测框中选取出最终的预测框。
- 接下来你就该对每个真实框标号对应的多个候选预测框做选择,选择常用NMS(none maximal suppress)算法。算法大概为,对每一种真实框标号对应的多个候选预测框做以下操作:
- 对每种类别的候选预测框crop的图片部分做softmax分类,对应类别/真实框标号的softmax输出值为该锚框的针对该类别的置信度(第一次计算出置信度后,可能还要设定一个不用太高的阈值,对这些候选预测框做一次预筛选)
- 将这些锚框的置信度排序
- 选出置信度最高的锚框,剔除出序列,作为最终预测框之一(事实上,nms算法选出来的每一个真实框标号对应的预测框一般有多个)
- 计算出序列中剩下的候选预测框和第(2)步选出来的预测框的IoU值
- 根据预先确定的IoU阈值,剔除掉IoU值大于该阈值的候选预测框,序列中剩下的候选预测框作为新的已排好序的序列
- 若是序列中仅剩下一个锚框,则nms完成,否则回到第(3)步继续。
- 第7步中你已经用nms从模型预测出来的大量候选预测框中选出了每个真实框标号对应的预测框。由于NMS算法的流程,你选出来的的bounding box的数量不确定,刚好就对应了一张输入图片中被检测物体数不确定的情况。还有就是,你做完nms后,得到的bounding box只是局部非极大相似锚框被消去了,局部置信度极大锚框被保留了,但你局部置信度极大,就一定达到够用吗?不一定,你可能还要设定一个置信度阈值,对nms筛选出来的局部置信度极大的锚框做一轮二次筛选。
总结:根据锚框进行目标检测和我们之前学的东西(例如图片分类)都不一样,有以下几个区别:
- 以前样本是大量图片,现在是一张图片的大量锚框
- 以前训练模型用的label是最终真实值,现在是与真实框相关的锚框信息(当然,最终你想要的真实值还是真实框)
- 以前模型预测出来的值就是你想要的东西,现在模型预测出来的值是锚框信息,你还要\(\to\)前景框\(\to\)候选预测框\(\to\)(nms)\(\to\)预测框
- 以前训练模型用的label都是数据集原原本本给你了的,现在label都是你要根据真实框手动给每个锚框打上锚框信息。
也就是说,数据是(图片,真实框)\(\to\)(锚框(前景框),锚框信息)\(\to\)训练+预测\(\to\)(锚框,锚框信息)\(\to\)(图片,真实框)。算法是:锚框生成算法\(\to\)前景框筛选算法\(\to\)偏移量算法\(\to\)【模型训练】\(\to\)锚框生成算法\(\to\)【模型预测】\(\to\)前景框筛选(一个步骤,不是算法)\(\to\)偏移量算法\(\to\)NMS。
锚框目标检测实例一:R-CNN
区域卷积神经网络,常常用来做锚框目标检测,我们这里就拿它来作为我们的“锚框用于目标检测”的一个实例。
一般R-CNN的算法流程是:
- 启发式算法搜索选择锚框
- 使用预训练模型(常常是CNN)来对每个锚框抽取特征,抽取出来怎样的特征怎么用?一种常见的做法是CNN输出一个矩阵,把这个矩阵拉成向量,即为feature map
- 训练一个模型(早年间常常是SVM)来根据特征对每个锚框crop的区域分类
- 训练一个模型(早年间常常是线性回归模型)来预测锚框对ground truth的偏移。
第1步锚框选择好后,第2步训练模型了,训练模型要解决的一个首要问题是把每个锚框crop下的样本batch化,但每个锚框大小不一,怎么batch?有种方法,把锚框均匀分割成nm块,输出每块的最大值——这叫nm ROI(兴趣区域)池化层,它的作用就是帮助批量化不同大小的图像。
RCNN流程再总结就是:启发式\(\to\)ROI pooling\(\to\)CNN锚框\(\to\)SVM+LinearClassify
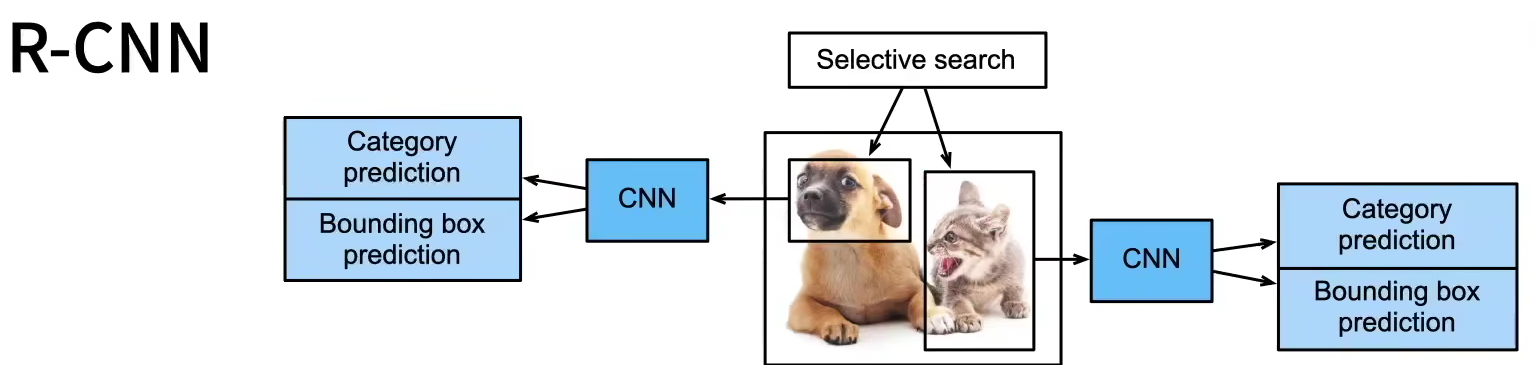
但上面的流程有个缺点,第2步要对每个锚框抽特征,计算量太大,于是我们提出了fast RCNN。改进是:
- CNN先对整张图片抽取特征,抽取出来的特征是一个矩阵
- 启发式算法选出锚框
- 锚框在原图上的区域映射到CNN抽取出来的特征上,等比例地crop下对应特征
- 锚框crop下的特征矩阵必然不能被batch化,这个时候要对特征矩阵做ROI池化,然后拉成向量
- 把向量送入SVM或线性分类器预测类别,送入线性分类器预测偏移量即可。
Fast RCNN流程再总结就是:启发式\(\to\)卷一下原图得到fetaure_map\(\to\)锚框crop掉fetaure_map\(\to\)ROI pooling\(\to\)SVM+LinearClassify。
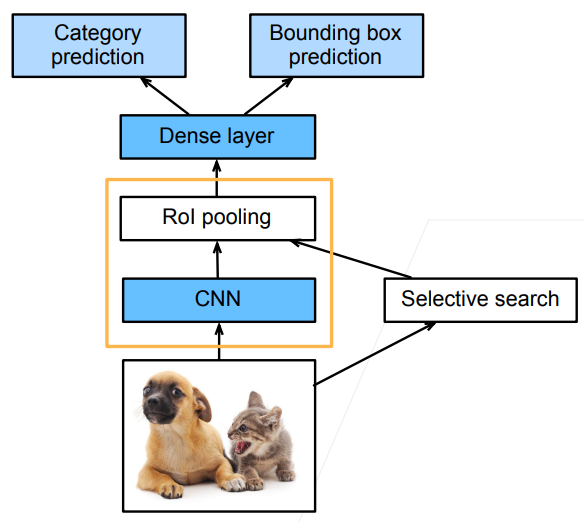
但有人还是觉得Fast RCNN不够快,因为启发式算法选锚框太慢了,所以提出来了Faster RCNN,具体不多讲,就是相当于用一个RPN区域提议网络替换了启发式算法,而RPN就是相当于一个糙一点的目标检测啦,我只解释一下下面这张图的RPN:
RPN中对CNN提取出来的feature map做了一次conv后,再次得到一个feature map,然后管你用启发式还是暴力生成锚框,反正接下来你得到了Anchor box一堆,然后再训练一个模型,预测你的每个锚框的锚框信息:是否框住了某个类别+离ground truth的偏移值,然后以框住了某个类别的锚框做NMS得到最终你要的锚框,离开RPN就是了,剩下的流程就是和Fast RCNN一样啦,映射锚框……ROI pooling……
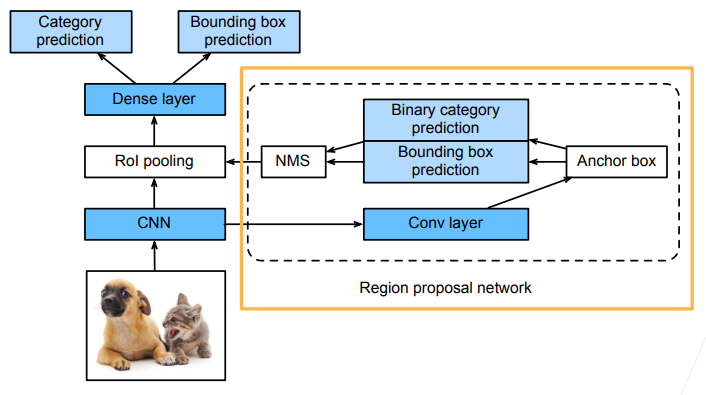
类似这种Faster RCNN的,先做一个糙一点的预测再做一个精准预测的一般被称作2-stage模型,即两步预测。
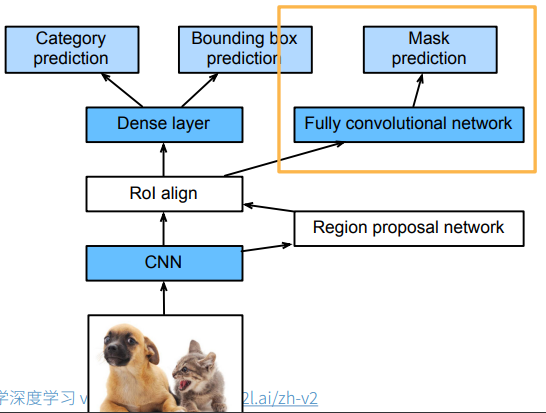
还有一种针对性能而非针对速度的改进,叫做Mask RCNN,我还是针对下面这种图讲解一下,它基本上是由Faster RCNN改进而来的,区别主要在:
- 该网络需要ground truth是mask像素级分类而非简单anchor锚框分类的数据集
- 在ROL后面加了一个FCN卷积网络,卷积出来的结果做预测,预测原图mask/每个像素的分类
- 预测mask并不是真的要它这个结果,因为这里通过CNN和ROI已经丢失掉很多原图信息了,不可能再得到精确的mask预测,这里预测mask只是为了让CNN和RPN表现得更好——这是一种重要的思想,有时候对一个模型的某个功能的训练只是为了使得它在其他功能处表现得更好
- ROI pooling改成了ROI align,因为原来的pooling对锚框做nm分割,像素是离散的值,例如对33的图像做22分割,分割出来的区域必然出现像素偏移,也就是说4个分割出来的区域的像素来源数量不均,分别是4,2,2,1,这对于mask prediction不好,因为mask prediction是对像素级别做预测,你这里产生像素偏移了,会影响mask预测结果,所以我们这里把pooling改成align pooling,对33的图像区域,对半切割它的第2列和第2行,切割出来的每小部分离散单像素按照一定权重分配给22的4个子区域,即得到22的ROI align pooling的结果。
很有意思,池化本来是想要通过模糊原图像素的方式来消除后层神经网络对像素抖动的敏感性,而这里用于要做精确的mask prediction,人家后层神经网络就需要这种对像素抖动的敏感性,所以你这里的池化不能像一般池化持有很糙的模糊掉原图的思想,而是在模糊的过程中也要尽量保持像素间的相对关系,支持后层对像素抖动的敏感性。
锚框目标检测实例二:SSD
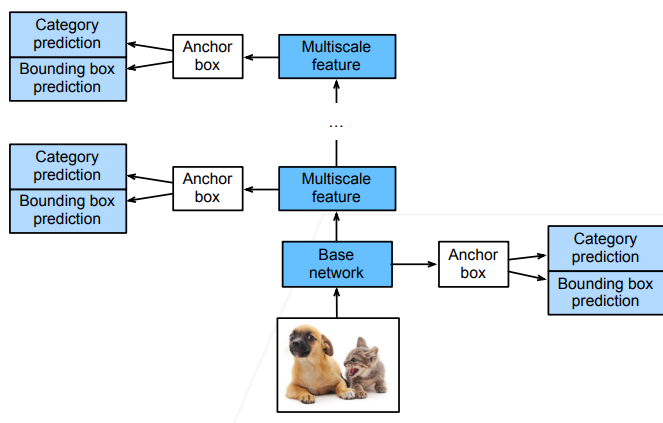
Single Shot Detection。可以译作单发检测,意思是最常用的RCNN都是2-stage,即一个主网络+一个RPN,麻烦,我SSD一发入魂。它的基本思想是通过多层的分辨率不同的网络叠加最终得到良好的效果。
SSD网络的整体架构分为多步stage(这里的stage指的是我们常常描述CNN用的那种使得feature map长宽减半的stage),每个stage上对于输入的feature map的锚框生成算法都是每个像素为中心生成多个锚框(但在实操时,你其实多半会采用均匀采样的方式在feature map的部分像素上生成锚框),但每个stage生成的锚框大小都差不多,这就导致了:每个stage输入进来的feature map大小不一,但锚框大小又差不多,于是下面的stage锚框框住的区域较小,适合检测小尺度的物体;上面stage锚框框住的区域较大,适合检测大尺度的物体。
总结起来SSD3大思想就是:
- 单神经网络检测模型
- 每个像素为中心产生锚框
- 多个stage的输出上进行多尺度的检测。
【由于是分层多尺度检测,假如你图像中的物体特别小的话,就把输入图片的size做大一点吧】【SSD,还有很多锚框目标检测算法的finetune有两种做法,一是用图片分类的pretrained_net来加上cls_pred和bbox_pred,直接利用图片分类的卷积层,而是把另一个ssd拿过来,但cls_pred和bbox_pred要大改,因为num_anchor和num_class都不一样了】
YOLO(you only look(live) once)是比SSD效果好,且更快,因为SSD中每个像素生成若干锚框,必然导致锚框大量重叠,浪费掉了很多计算,而YOLO将图片均匀分为S*S个锚框,每个锚框再预测多个ground truth边缘框。
我已看完SSD pipeline李沐代码实现,接下来我将就自己对其代码的理解讲解一下SSD的详细结构,帮助你自己手写代码。有些细节处可能和李沐的代码不一样,但道理相通。下面是一张基本的SSD结构图:
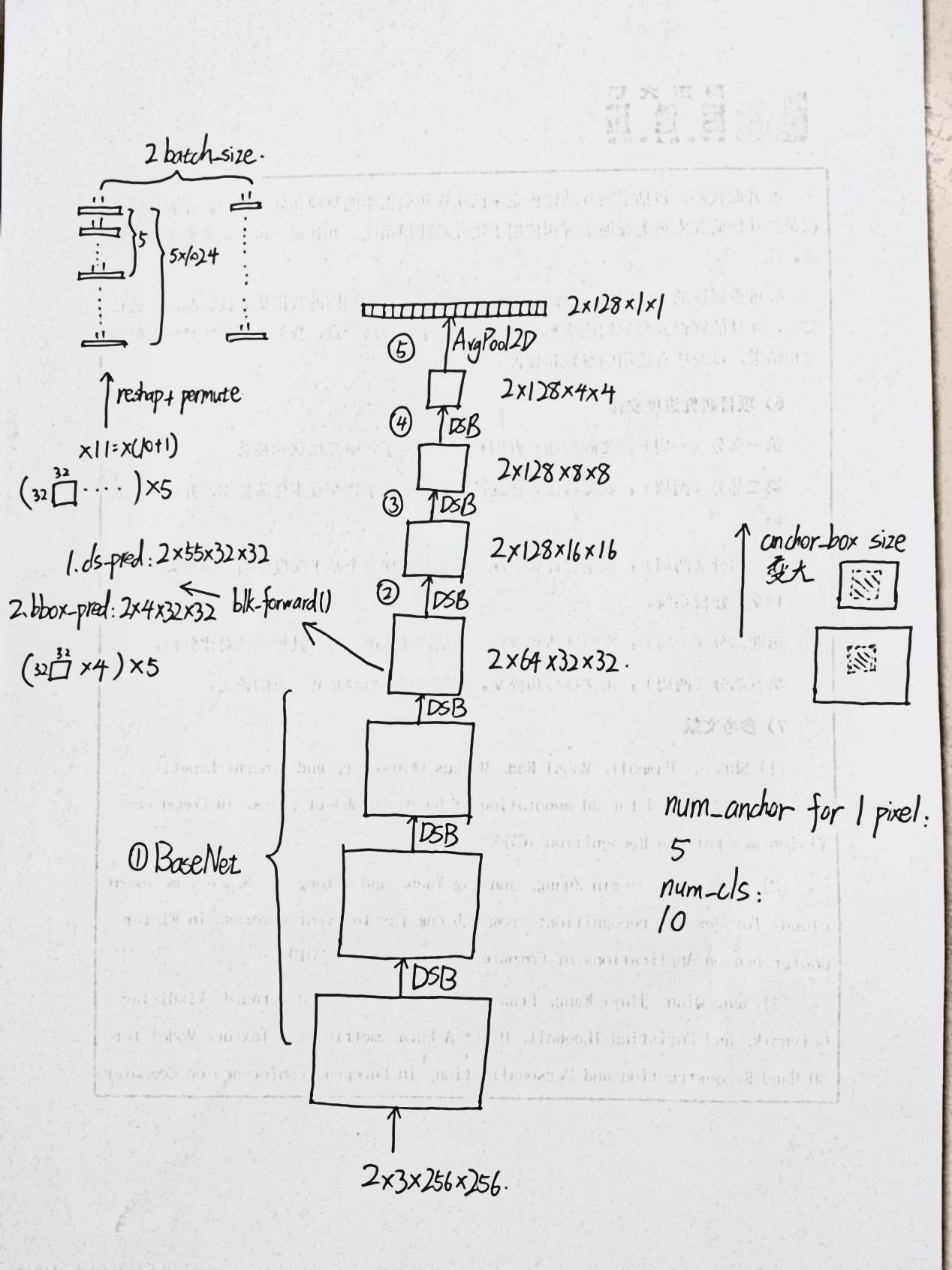
它有5个stage(不是使长宽减半的stage),其中第一个stage称作basenet,就是从feature map刚输入到第一次输出的feature map被用于做锚框信息预测的stage它就是普通的卷积,由3个DSB构成;第2、3、4个stage都是DSB,DSB就是down_sample_block的缩写,它就是一个普通的conv,第5个stage是一个池化层,将第4stage的output flatten成一个一维张量。
锚框是事先就生成好的,而不是在模型推理过程中根据feature map的大小生成好的,也就是说,你在构造模型的时候就该知道每一层的feature map长宽是多少。生成锚框的算法有大小形状两个重要参数,size数组和ratio数组,s是0~1之间,ratio反映长宽比例,它们都无量纲。对于每个stage输出的feature map,都会有不同的size和ratio参数,ratio参数其实可以不同stage都一样,但size数组从下到上就要逐渐增大,这才符合SSD多尺度目标检测的原则。注意对于每个feature map来说,最终根据s和r生成的每个锚框有4个参数,分别是左上和右下角的坐标。
每个stage输出的feature map要加上两个CNN,一个是class_pred,一个是bbox_pred,分别预测每个锚框的类别信息和到真实框的偏移量信息。它们输入都是feature map,输出的话,cls_pred的通道数应该是“每个像素生成的锚框数”(“预测的总类别数”+1),”+1”是代表对背景框的预测;bbox_pred的通道数应该是4,代表到真实框的4个坐标的偏移量。要注意cls_pred和bbox_pred输出的也是feature map,大小必须和输入的feature mao一样!为什么要怎么干?拿第1个stage输出的feature map的cls_pred举例,它输出了5(10+1)=num_anchor(num_cls+1)个feature map,num_anchor是每个像素要生成的锚框数量,feature map3232,3232是输入的feature map的像素个数,也就是说,cls_pred要针对3232个像素,每个像素生成5个锚框,每个锚框预测11个类别的评估分数,所以一共应该有323255=3232511个单个输出数据,这3232511个单个输出数据如何表示?如何表示决定了其该如何从输入的feature map中计算出来,我们采用了CNN中最方便的输入输出数据表示方式,即是也用feature map表示,3232天然可以对应于输出的feature map的大小,55可以分为5组,代表该输入的feature mao根据s和r计算出来的应该生成的5类锚框(每个像素生成的5个不同大小形状的锚框),每组有11个feature map,也就代表了3232个像素预测的5种中的一种锚框所预测的11个类别值,5个分组也就代表了3232个像素预测的5种锚框的没种11个类别预测值。bbox_pred的输出也是一样的道理,只不过它的每个像素预测的不是11个类别,而是4个偏移量。那么你就要问了,上述cls_pre和bbox_pred好像对于一个feature map预测出的类别信息和偏移量信息跟生成的anchor没有任何关系?也就是说,它们作为卷积层,输出的整个feature map看到的视野是整个输入的featrue map(或者严格细致一点来讲,每个输出的feature map的一个像素代表的是一个锚框预测的某一个类别评估分数,或者某一个偏移量,但它们的预测数据来源所覆盖的输入feature map的范围是blk_forward卷积核的大小,或许是33,但肯定不是对应输入像素的对应锚框大小),而不是5组输出分别对应的锚框的视野,跟生成的预先anchor没有如何关系,这是怎么回事呢?其实啊,我们在infer时确实没有让预测的class和bbox与看输入的feature map的锚框视野,而是稀里糊涂地去卷积就完了——但我们在train时会用根据预生成的anchor所打出来的groud truth去训练CNN的参数,强迫cls_pred和bbox_pred去看对应锚框的视野。那么接上另一个问题,就算是train时强迫cls/bbox_pred CNN去看对应锚框的视野,但在卷积时,输出的feature map的单个值也绝对绝对只能覆盖掉33的范围(假设卷积核大小是33),不可能覆盖掉锚框的视野啊?这里,就体现出BaseNet先用DSB做了多层卷积的重要性了,你cls/bbos_pred名义上是说看的是每个stage输出的feature map的锚框视野,但说到底是要看最开始输入的image的锚框视野(虽然没有针对它生成锚框),所以BaseNet的3个DSB已经把image的像素信息都给你混匀了,你kernel_size=3*3,但看到的仍然是更大的视野——针对每个stage输出的feature map生成的锚框的本质其实是多尺度地看image中的信息。
于是上述还引出一个问题,给你一个数据集,里面的每张图片打好了bounding box的位置和class,bounding box的数量不固定,位置不固定,class不固定——所以,你就要根据每个像素生成的大量锚框运用前景框筛选算法+偏移量计算算法,给每个锚框打上锚框信息,这才是你最终训练时用的groud truth的数值——预先生成的anchor最终也就在这里起到了训练作用当然。你模型训练完做推理时也要用同样的size和ratio生成大量锚框,比较cls_pred和bbox_pred生成的只是锚框类别和偏移量,你还要根据类别筛选出锚框,用偏移量+锚框计算出真实框,在用nms得到最终的真实框。你训练模型时既然是用了这一组size和ratio生成的anchor,那你完了预测时,也要用同一组anchor——这也就是为什么基于锚框的目标检测算法的模型微调不容易的原因,一个pretrained_net基于的锚框都跟你的不一样,所以微调还不如干脆用图像分类CNN中的卷积层拿来微调,甚至pretrained_SSD的主干上的BaseNet和DSB都不适合拿来微调,因为它们提取特征是为了让后面的cls/bbox_pred看到更大的锚框视野而非kernel_size,pretrained_SSD铺开的锚框视野是每个像素10个锚框,锚框形状稀奇古怪,但假如你想要的是每个像素3个锚框呢?对吧。
所以,SSD模型超参数不仅仅是kernel_size+padding+stride+层数+输入输出通道数,还有
- 锚框是针对每个像素生成还是等距采样
- size
- ratio。 你微调,大不了迁移过来改一下层数,其他的你什么也改不了,关键是后3种超参数还对SSD十分十分重要,你怎么兼容pretrained-traing?不像kernel_size和输入输出通道数这些,前者反正是提取特征,后者也能用数据预处理解决pretrained-training不兼容问题。</span>
说到groud truth的数值,还要说说它的表示。对于class,每个像素的每个锚框会有一个真实值,而不是11个评估分数,所以,class_label应该是长为sum_anchor1的一维向量(sum_anchor=32325+16165+……),bbox_label应该是(sum_anchor *4)1的一维向量(就不用sum_anchor4的二维矩阵了,虽然语义上好理解,但是这种数据表示的话,pytorch提供的损失函数不好算它)。所以,你就要对你cls_pred和bbox_pred预测的553232和43232(以第1个stage为例而已是3232)做.permute函数维度变换,变换成(511)1024\(\to\)115120\(\to\)512011(把55分割成511没问题的,训练时会强迫你5个里面每个11都是预测的一个锚框的11个类别的评估分数,让5*11的分割不是胡乱瞎分割乃由train过程来诱导实现。分割的过程由.reshape函数实现),其他stage上的clas_pred结果照例,最终把全部stage上的cls_pred预测值都cat成sum_anchor11,与class_label做交叉熵,得出cls_pred的loss1。bbox_pred则是将43232直接转换成4096*1,与bbox_label求出loss2。加权求和得到最终的loss。
你训练时算损失函数是把cls_pred和bbox_pred的结果做了reshape、permute和concat(concat的是不同stage经reshape和permute后的结果),但是你最终模型在预测用是,的出来的结果还是不同stage feature_map的55wh与4wh,你应该写一个函数predict对它们做进一步的提取得到最终的bounding box的类别与坐标。
要注意在对bbox_pred和bbox_label求loss2的时候,要对两个数据都乘以一个bbox_mask(里面的值只有0和1),因为cls_pred预测出来的类别最终决定了选取哪个锚框作为前景框,只有前景框的bbox_pred才是有效的,背景框的bbox_pred与bbox_label全部置为0,不参与有效的损失函数计算。但是你是在训练啊,你cls_pred根本没训练出来,你怎么知道那些锚框是前景框背景框那些bbox_pred值是有效的?也就是说,你bbox_mask是怎么确定下来哪些值为0哪些为1的?对了,我们不是有groud truth吗,你就把groud truth里的前景框对应的bbox_mask的值置为1就行了,就用真实值对应的bbox去训练bbox_pred就行了,不用管训练时的cls_pred。我打比方:对于锚框a,你最后训练出来,cls_pred认为它类m的前景框,但groud truth不是,所以bbox_pred训练用bbox_mask把对应锚框的bbox_pred预测值置为了0,没参与训练。所以你对a上偏移,得到所谓的真实框,但这个真实框的框住的是一个乱七八糟的东西,对它框住的内容做softmax分类,对m的置信度极低,nms一上去就先预筛选把它给剔除掉了。所以,你训练时,cls_pred不影响bbox_pred的label又怎样?So What?
我还想补充几点:
- 我们前面说SSD是多尺度多stage生成锚框的目标检测,我们又说过目标检测中每个锚框是一个样本。我们这里的例子中的样本是一张image进来后,每个stage所有的锚框,毕竟你最终训练时也是将所有锚框的预测值concat到一起来训练的。也就是说SSD最终的输出是每个stage的所有锚框在一块儿,而不是选出几个stage的锚框作为输出。其实我想到一个idea,就是我下面的size比较小嘛,我检测电线杆,我上面的size检测大象,也挺好,反正你的cls_label是由groud truth和anchor计算出来的,你每一层都会由不同的size和ratio生成不同的anchor,不同stage的anchor根据本stage负责检测大象还是电线杆去针对性地打上label。当然你这样干的话,stage电线杆cls_pred可能是(5(3+1))3232,stage大象cls_pred可能是(5(5+1))1616,类别变了嘛,类别数也可能变——于是在计算损失函数时你就要解决一个问题:原本要把cls_pred的结果reshape+permute+concat成sum_anchor4,这下可好,你一个stage可以拼成sum_anchor4,另一个只能拼成sum_anchor*6,你怎么把不同stage再拼在一起算loss?可能只能不同stage分别算loss然后加起来了。
- 每个stage可能针对每个像素的锚框生成的个数都不一样,例如stage1 cls_pred出来是(511)3232,stage2则是(311)1616,但这不影响,在算损失函数时你保证11==11就能让不同stage的全部锚框拼接起来就行。
- 往往为了简化计算,我们对一张feature_map可能不是每个像素都生成锚框,可能给一张3232大小的图片,我们告诉算法说,诶,我这张图片的大小是2020,那就让算法给你生成2020num_anchor个锚框吧。于是,cls_pred出的结果可能就不是553232了,而是552020,但由于都是预测11个分类,所以55==55\(\to\)11==11,最后训练时算loss能reshape+permute+concat成标准的sum_anchor*11的形式。
- 综上,cls_pred和bbox_pred的数据维度表示影响的只是损失函数的计算形式,其实只要你仅仅保证每个stage的所有锚框预测的类别数是一样的,那就没有任何问题,最终算损失函数不同stage全部锚框预测值拼在一起算,不会出现拼接时维度冲突的问题。
- 注意stage5的一维向量,似乎没办法用cls_pred和bbox_pred做卷积了,但其实不然,你用padding=1、kernel_size=3*3照样可以做卷积。
语义分割:
对于语义分割数据集而言,有feature和label,feature是模糊点的.jpg都没有问题,label必须是无损模糊少的至少.png。一份语义分割样本,feature和label的大小是一样的,若是你想改变图像的大小,你只能crop不能reshape,因为reshape涉及像素间的插值,两个像素,背景是黑色,mask是红色,你怎么插值,你难道要把它插成粉红色吗?
语义分割使用转置卷积神经网络,早期的网络叫做FCN(全连接卷积神经网络,我也不知道它跟全连接层有什么关系),FCN核心思想就是先用CNN对input抽取特征,size压缩变小,然后加上转置卷积层把feature map放大到原来的input大小,此时output有n个channel,像素在每个channel的值代表一个类别的评估分数,损失函数宜用交叉熵损失函数。用于语义分割的网络必须满足像素到像素的映射,假如我们使用样式迁移的思想来做语义分割,原图是feature,样式图是label,则不能用于语义分割,因为它不满足像素级别的映射,只有转置卷积满足像素到像素的映射。
转置卷积:
首先明确:转置卷积不是对卷积的还原,虽然你可以说它是还原了size,但绝对不是为了还原value。
我认为转置卷积不如叫做逆卷积(事实上转置卷积在DL中也常被叫作反卷积,但反卷积其实是数学上的概念,它同时逆变换了size和value),首先你通过矩阵乘法的角度来看卷积,早期为了兼顾计算资源,把卷积运算改造成矩阵运算,即是将输入输出都拉成向量,\(Y^{m\times 1}=V^{m\times n}X^{n\times 1}\),V是卷积核,其中输出Y的m必然大于等于输入n。但转置卷积则不一样,它是\(Y^{n\times 1}=V^{n\times m}X^{m\times 1}\),输出m小于等于输入n,有人认为就说\(V^{n\times m}\)相当于把 \(V^{m\times n}\) 转置了,但我认为不如说是把\(V^{m\times n}\)乘到左边去,作为一个逆运算,所以不如叫逆卷积。
而且从非矩阵运算的原始直观卷积运算来看,转置卷积也更像是对一般卷积的一次你运算,你画个图试试,比较一下二者的stride的形式,是不是就很好理解。
那么问题来了,computer scientist为什么一开始就是要把反卷积叫做“转置卷积”呢?原因如是:我们说了卷积操作可以用矩阵和向量的乘法得到向量来表示,设定卷积核为K,当它用来做正常卷积时(我们默认padding=0,stride=1),它的矩阵形式是W,那么,当它用来做转置卷积时(此时输入输出向量的大小刚好和正常卷积时相反),它的矩阵形式是\(W^T\),而不是\(W^{-1}\),所以叫装置卷积——所以我们还知道了,当我们用正常卷积核K把向量X变成向量Y时,再用同样的卷积核对做转置卷积,并不能把向量Y通过逆阵逆变换成X,所以用K做的反卷积叫做“转置卷积”而非“逆卷积”。所以我们有了一个转置卷积核对应的矩阵的计算方式(这个计算方式是我想出来的,现实中基本不会用到,但在下面我对自编码和自解码器理解中能起到帮助):当给你一个转置卷积核时,
- 你肯定(默认padding=0,stride=1)能得到其输入feature map Y和输出feature map X的size(这里我们只关心size,好计算W的size应该是怎样,才好在该W size中填入K的元素值。\(W^T\)在W非正则情况下是不可能把X再还原为Y的)
- 然后你先求它对X做正常卷积所对应的矩阵W,好求
- 接着把W转置,就是\(X=W^T Y\)中转置卷积对应的卷积核\(W^T\)了。
要注意对于一个卷积核K来说,若是其正常卷积矩阵乘法表示有\(Y=W\times X\),那么K做转置卷积必然有\(Z=W^T X\),\(Z\neq Y\),\(Z\neq Y\),\(Z\neq Y!\),除非W是正则的。
你还要注意转置卷积的padding,当ConvTranspose2d函数的padding参数为0,stride参数1,kernel_size=22时,且input size=22时,output会是33(你可以理解为33的output被22正常卷积后会成为22的input),但若是把padding设为1,则output会变成11,则是为什么呢?明明正常卷积的话,这种情况output应该会是55啊——错了,你还是要按照output正常卷积为input的思路去理解,想象怎样一个output在加了padding之后会被22的正常卷积kernel卷成22?那必然是1*1的卷积啊——后面再实际计算过程中,你遇到ConvTranspose2d padding=n,直接把转置卷积的output size外围去掉一圈padding就行了。
如果说卷积的输出是模式匹配产生的响应,那么转置卷积的输出就是这些响应在空间上更细粒度的分配/具象表达。这种再分配/表达不是按某种规则恢复出来的,而是学习得到的。转置卷积也可以看做一种上采样的方式。在转置卷积的时候,kernel_size最好还是大于stride,这样能使得每从输入卷一个像素得到的map之间能够有一定的重合——为什么要这么做?有一种不太恰当的理解(毕竟转置卷积逆变换的只不过是size):假如我们把转置卷积的inputY看作正常卷积的输出,output X看作正常卷积的输入,则对于正常卷积而言,X的1个像素为Y中多个像素提供了信息,那么当转置卷积要从Y逆变换为X时,就要对X中一个像素从Y中多个像素抽取信息来供养,则必须使得转置卷积核对Y中相邻两个像素卷积出来的map映射到X上有所重叠,所以应该stride < kernel_size。
其实你早就理解了转置卷积的计算方式,不就是卷积核对每个像素做计算吗,然后把计算结果按照步长来堆叠吗,然后把输出去掉外围一圈padding吗,但是这对于计算机而言,代码实现可能会变难,所以有更简便通用虽然人类直观不太好理解的方式:
- 当填充为p步幅为s时
- 在行和列之间插入s-1行或列
- 将输入填充k-p-1 (k是核窗口)
- 将核矩阵上下、左右翻转
- 然后做正常卷积 (填充0、步幅1)
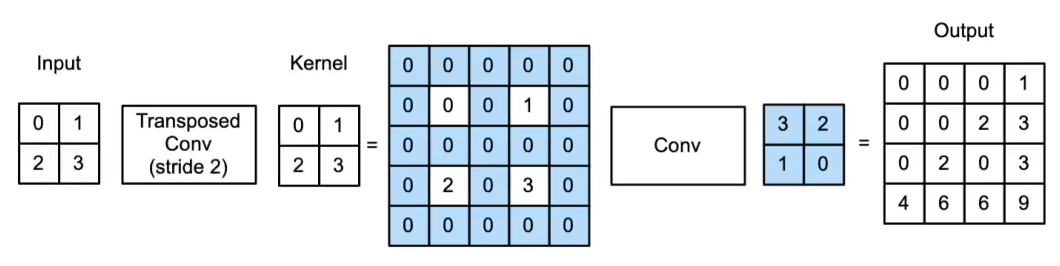
所以我觉得,你对一个feature map做卷积后再做转置卷积(两个卷积核不一样),相当于自编码器+自解码器。而且显而易见,你要是想让自编码器的结果完美还原为自编码器的输入,则自解码器的卷积核对应的矩阵必然得是自编码其卷积核对应的矩阵的逆阵(应该是伪逆),所以自解码器的卷积核对应矩阵必然会在训练过程中无限逼近自编码器的逆阵,若是此时恰好自编码器的卷积核对应的矩阵是正则的(逆阵==转置),则自解码器的卷积核对应的矩阵将既是其逆阵,又是其转置——结合我们上面讲的为什么转置卷积会叫做“转置”卷积即转置卷积核对应的矩阵的计算方式,我们可以知道转置卷积核必然与自编码器卷积核完全相同——因为如果一个卷积核K的对应矩阵W能将Xsize的向量转化为Ysize的向量,那么其转置\(W^T\)必然能将Ysize的向量转化为Xsize的向量(我们这里只关心size),且\(W^T\)对应的转置卷积核必然也是K!
我想,我们最后在不断训练这个自编码器+自解码器的卷积核转置卷积核时,训练的结果应该也是让
- 自编码器卷积核对应的乘法矩阵越来越正则
- 转置卷积核则相应地和卷积核越来越一致。</span>
转置卷积核初始化:
转置卷积核像一个上采样,或者我们可以说,它把一个图像放大了,把图像放大,我们常常使用双线性插值算法。在实际使用转置卷积层时,为了缩短训练时间,我们常常会预先初始化转置卷积层,我们让它的初始值就表现得像一个专门用于双线性插值的。为此我们会写一个函数,专门用于初始化转置卷积核使其具备双线性插值的功能,这个函数具体怎么实现就不细说了。
样式迁移:
样式迁移是个很简单的东西,按照李沐讲的代码pipeline,首先你要有一张原始图片,一张样式图片,一张待训练的目标图片——没错,你训练的不是网络的权重,你训练的是目标图片的像素值,目标图片的初始像素值可以随机生成,也可以直接取原始图片像素值。
接着你找来一个resnet,这个resnet是现成的pretrain好了的,它对原始图片和样式图片提取特征,你把它对原始图片提取到的某些卷积层的feature map作为目标图片的content label,你把它对样式图片提取到的某些卷积层的feature map作为目标图片的style label,然后在把这个resnet作用到目标图片上,提取出对应conv层输出的content feature和style feature,接着你就可以计算出content loss和style loss了。
关于损失函数,content loss好说,直接比较每个像素的相似性即可,L2范数。对于style loss,显然你比较每个像素相似性并不合适,你应该比较style feature和style label的统计信息间的相似性,统计信息常用gram matrix表示,计算出feature和label的gram matrix,如何计算很简单,不讲。损失函数还应该包含第3个部分,就是平滑损失,反映了目标图片平滑程度,也就是不要噪点,计算平滑损失直接在目标图片上计算即可,不用resnet提取feature map。总损失函数包含3个部分就是了。
上述是原始的样式迁移算法,你每要生成一张目标图片,都要重新训练一次目标图片,这不好,所以现在的样式迁移算法都会额外训练一个CNN来infer出目标图片了,具体实现不讲。
自编码器(AE):
自编码器不是NLP中的编码器-解码器架构。
AE是一个无监督学习模型,简单的AE只有3层,其中隐藏层的大小往往小于输入和输出层(输入层大小等于输出层),AE起到的是一个数据压缩,或者说,提取输入关键特征的作用,提取出的关键特征被隐藏层输出,然后给了输出层。所以在实际使用中,我们训练好了一个自编码器,往往把它的输出层去掉,输出层只是单纯用来无监督训练用的,我们把自编码器的输入层+隐藏层保留,给其他神经网络使用。
很多AE的隐藏层大小都小于输入输出层,但稀疏自编码器SAE是个例外,它的隐藏层大小大于输入输出层,为什么这样干?不是要数据压缩/提取关键特征吗?这样干明显不合理。所以这样干的原因是,人们想要模拟大脑机理,人们发现大脑在收到外界刺激后,大多数神经元是被抑制状态,不会传递出激活的信号——于是人们就想让SAE的隐藏层大一点,模拟大脑容量,但在训练过程中按照一定法则诱导隐藏层大多数神经元的活性处于抑制状态,训练出来的模型参数也就模拟了大脑机理,使得输出的张量大多数值为抑制/非激活状态,也就是0。所以叫“稀疏”自编码器。而由于编码结果虽然比输入的张量大,但由于其稀疏,所以起到了和AE一样的数据压缩的作用。
是怎样的法则使得SAE训练时能诱导大多数神经元活性被抑制,输出接近0的数值?这需要我们对神经元激活/抑制做进一步理解——神经元的活性的评判规则是它对于不同输入产生的输出值的分布,神经元输出值越容易是0,则活性越低,越容易不是0,则活性越高。稀疏性就是指神经网络所有神经元的活性。举例就是:当神经元的的输出接近激活函数上限时(例如对于Sigmoid为1)称该神经元状态为激活,反之当神经元的输出接近激活函数的下限时称该神经元的状态为抑制,那么当某个约束或规则使得神经网络中大部分的神经元的状态为抑制时(也就是我们想要的SAE的效果),称该约束为“稀疏性限制”,稀疏性限制,是对神经网络模型参数的限制,使得神经网络稀疏性变强。我们对SAE的稀疏性限制的手段是:在训练SAE时,给损失函数加入一个惩罚项,诱导模型参数达到一个使得神经元活性在大多数输入情况下被抑制的状态。这个惩罚项是一个函数,该函数的输入有两个:
- 对神经元活性的度量(反映神经元输出容易为0的程度,由神经元输出值计算来)
- 神经元活性的理想期望。惩罚项计算出两个输入的偏差即可。惩罚项的细节涉及数学知识,这里不再赘述。
图神经网络:
即是输入时一张图,输出也是一张图。
现实中的几乎所有数据都可以抽象成图。
我们使用图神经网络首要解决输入输出的图的数据表示的问题,理想的图表示方法应该满足:
- 每个点/边/全局有一个属性向量来描述之
- GNN更新图的每个属性向量,但图的形状,或者说是点和边的连接关系不会被改变(这一点是GNN的基本假设,叫做“对称性”,如同RNN基本假设是时间延续性,CNN基本假设是平移不变性+局部性)。
关于第2点,普通的邻接矩阵就绝对满足不了,因为你要是交换两个点之间的下标顺序,就会得到一个完全不同的邻接矩阵,GNN会识别成不同的图,这不合理。
为了满足上述两点,且保证存储图(往往邻接矩阵稀疏)的空间不会过于庞大,我们把图的数据结构划分为4块,即顶点列表、边列表、邻接列表、全局信息列表。邻接列表中每个元素是一个二元组,有两个序号,序号是对应顶点在在顶点列表中的下标,每个二元组在邻接列表中的下标与对应边在边列表中的下标一致。于是:当我们改变顶点在顶点列表中的下标顺序时,只需要修改邻接列表中每个二元组的元素值即可;当我们该表边在边列表中的下标顺序时,只需要修改邻接列表中每个二元组的下标顺序即可。我们还要注意的是:顶点列表、边列表、全局信息列表中每个元素存储的值是对应顶点、边、图的属性向量(不同中数据的属性向量的长度不一定相同),所以,这些列表,本质是一个二维张量,但全局信息列表往往只有一个属性向量,表示本图的属性。
最基础最简单的GNN是,把点列表、边列表、全局列表(邻接列表往往不直接作为网络的输入,它只是起到确定并维系点和边关系的作用)分别输入各自的MLP,各自输出值,每个MLP互不干扰。这是最简单的。
但是这种最简单的GNN没有利用好图的空间信息。我们如何在GNN中利用图的空间信息?我们要把几个MLP整合起来,每个MLP每层layer处理各自列表前,各自列表的元素的属性向量会先受到其他列表的元素的属性向量的影响(带有这种性质的GNN又被称为GCN),怎么个影响法呢?首先明确几个术语(这几个术语是我暂时总结的,可能是偏狭错漏的),这几个术语描述的功能都是针对顶点/边/全局列表来操纵的,但却要利用邻接列表:
- 汇聚。举例,当你不知道一个边的属性时,你把与该边相邻的点的属性加和起来,作为该边的属性向量。“汇聚”的定义比下面几种定义都要明确而可信,它强调弥补缺失的属性向量。
- 信息传递。举例,当你不知道一个点的属性向量时,你就把与该点相邻的所有点的属性向量加和起来,作为该点的属性。
- 更新。举例,你可能知道一个边的属性向量,但是你还是通过某种方式将与该边相邻的顶点的属性向量整合进该边的属性向量。
上述几种操作的本质都是:一个元素的属性向量通过某种方式(常常是简单加和,也可以是求平均、求max)被另外的元素(通常是多个元素,且可能来自被更新元素不同的列表)的属性向量更新(可以是叠加到原属性向量上,也可以是直接替换)。
要额外注意的是,我们上面解释的这几种术语(可能是我编造的,更新、汇聚、信息传递等名词我们常常混用,反正它们本质一样),在GNN中用的最多的是“更新”。“更新”举的例子是相邻的点和边的信息相互更新,但实际上,若每层GNN的layer仅仅靠邻接列表表示的“相邻”关系来更新点和边的属性向量的话,未免有点局部了,我们每层GNN更新属性向量想考虑全局的图,如何考虑全局呢?注意我们上面的更新没有利用全局列表,现在用它:每层GNN分别处理各列表的元素的属性向量前,要对属性向量的值做更新,更新的边的数据来源是点和全局;更新点的数据来源是边和全局;同时我们还要用点和边的数据去更新全局——如此,便实现每层GNN了图的顶点和边列表的属性向量更新受到了全局的影响而非仅仅是相邻顶点和边了。
GNN和CNN有异曲同工之妙的地方在于,就算不传递全局列表的信息,只要你每层有对各列表属性向量的汇聚/更新,那么你的层数足够多的话,最后网络输出的值看到的数据就是整个图的数据,而非仅仅某个顶点与其相邻的顶点或边(这就跟卷积核的感受野一个道理,所以GNN的汇聚也被称作“图卷积”。其实当汇聚的方式是简单求和或平均时,这种图卷积也相当于对邻接矩阵做矩阵乘法,你自己想是不是这个道理)。那么,output的数据来源变多了,最后反向传播训练网络时的求导开销就会很大,所以我们在推理的时候不应该对每个列表的每个属性向量都做汇聚/更新,而是对各列表的部分元素做采样,采出来的属性向量做一下汇聚/更新即可。但令我疑惑的是,采样的方式李沐只讲了随机采样,而且随机采样也可以玩很花,例如随机游走、宽度遍历。汇聚时随机采样一些点做汇聚在训练时很合理,如同drop_out一样,但在训练完推理时呢?也是每层GNN对各列表的属性向量随机汇聚吗?这恐怕不合理,我不懂。
图神经网络的门槛很高,它对超参数特别敏感,而且训练起来非常贵,而且很难做到批量训练,因为你一个batch的图要是长不同的形状,那么它们的各列表的长度就是不一样的,你要如何统一各张图的表示,让它们成批量地输入GNN呢?这很麻烦。
GNN,或者说GCN的基本推理过程,总结起来就是:纵向来看GCN可以看做3个分开又彼此相连(通过邻接列表辅助的汇聚操作确定它们的相连关系)的的MLP;横向来看每一层GCN先对上一层输出的各列表的属性向量做一次汇聚(这里说汇聚不一定准确,它强调弥补缺失的属性向量,应该还要加上更新,或者笼统来说,信息传递),然后在上神经元做W*X。