Based on screw theory
Beginners, continuously updated …

INTRODUCE

Preliminary

本课程介绍的很多概念都是以以下 2-link planar open-chain 为例：

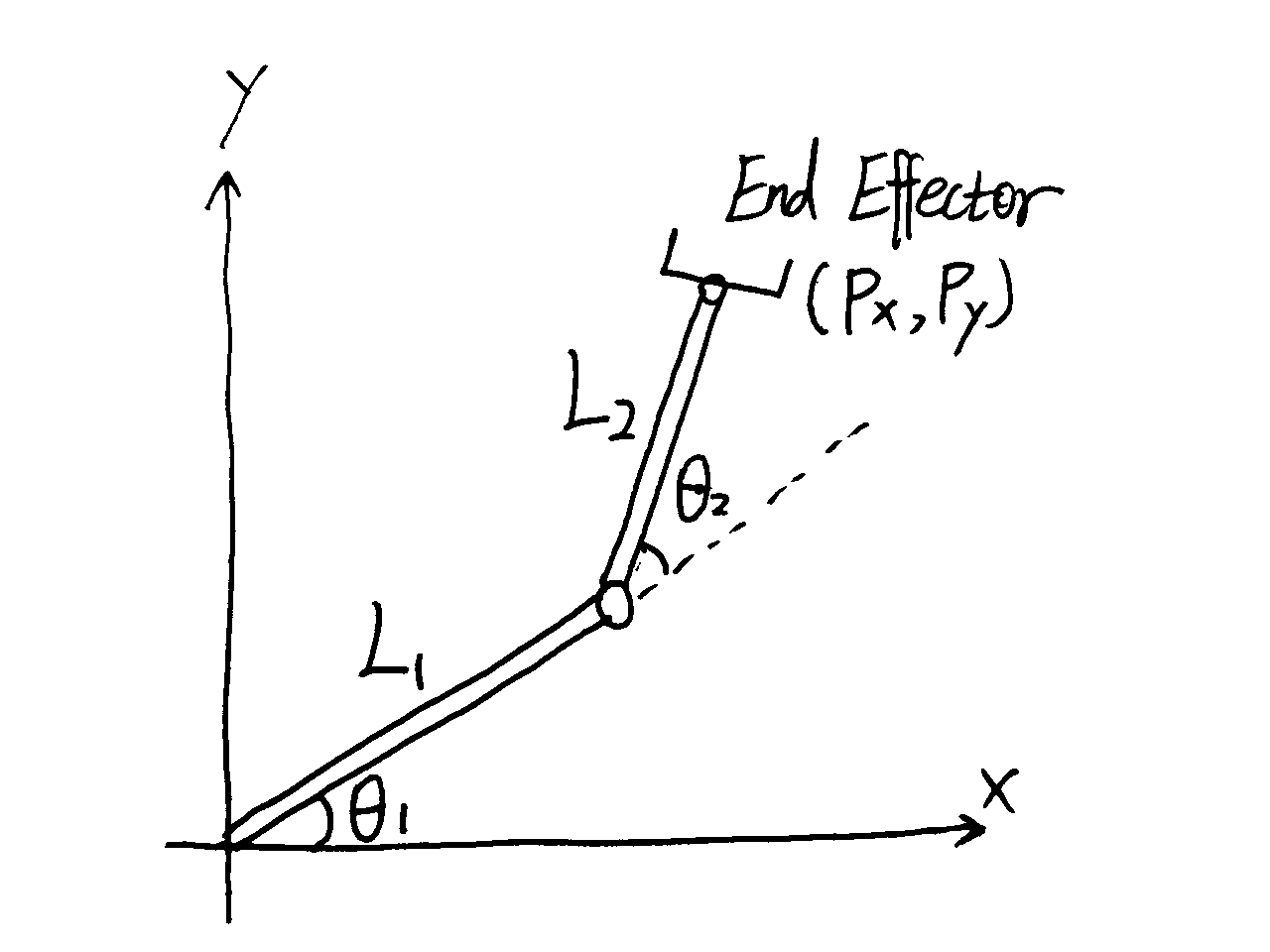
2-link-planar-open_chain

且我们常记： \[ \frac{\partial{P_x}}{\partial{t}} = v_x \\ sin(\theta_1) = s1 \\ cos(\theta_1 + \theta_2)=c12 \\ \frac{\partial{\theta_1}}{\partial{t}} = \dot{\theta_1} \] 以此类推

除了上述的 open-chain, 还有 close-chain:

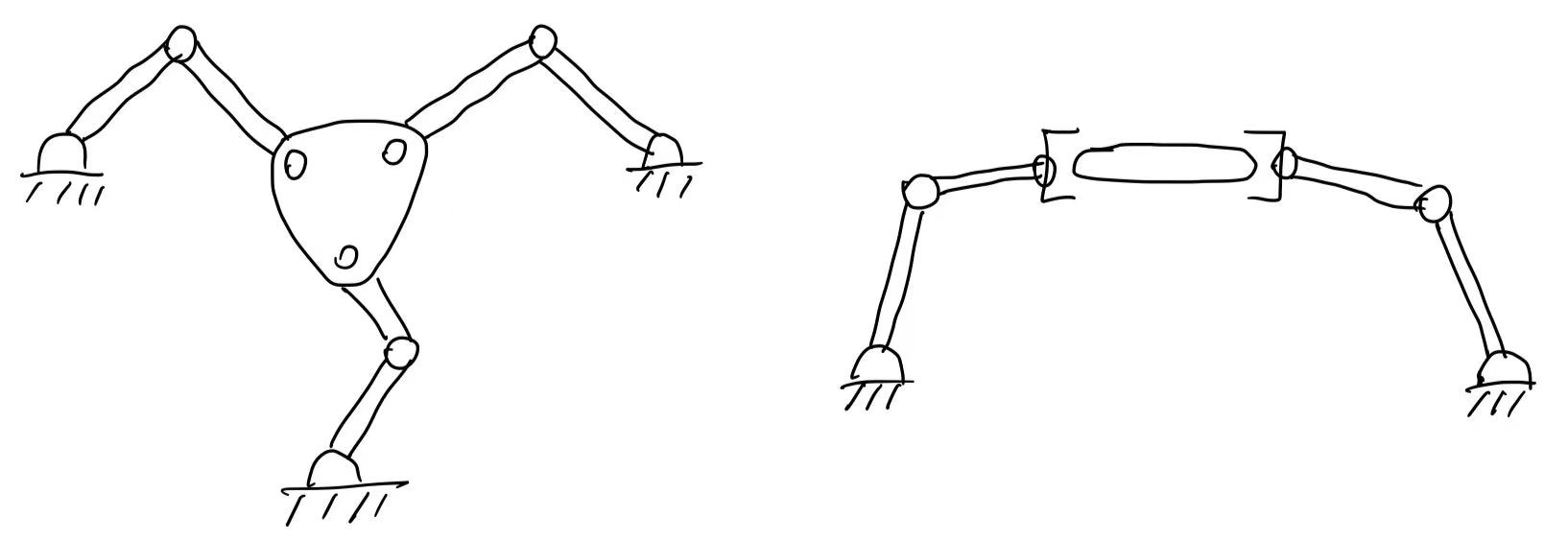
close_chain_intro

close-chain的雅各比矩阵奇异性非常有趣，我们后面会讲到。

Forward Kinematics

如2-link planar open chain图示，由\(\theta_1,\theta_2\)得到\(P_x,P_y\)就叫Forward Kinematics. \[ P_x=L_1 cos\theta_1 + L_2 cos(\theta_1 + \theta_2) \\ P_y=L_1 sin\theta_1 + L_2 sin(\theta_1 + \theta_2) \]

Inverse Kinematics

如2-link planar open chain图示，由\(P_x,P_y\)得到\(\theta_1,\theta_2\)的过程就是Inverse Kinematics.也就是解Forward Kinematics中的那个方程。

对于图示的2-link planar open chain 而言，解的数量最多有2个，而对于有些open chain，例如3-link，则解的数量可能有无数个(参照人手抓取物体)。

Jacobian Matrix & Singularity

我们控制机械臂去抓取某个坐标处的物体，肯定不是直接控制的\((\theta_1,\theta_2)\)的值，而是控制的\((\theta_1,\theta_2)\)其值的变化速率\(\frac{\partial{\theta}}{\partial{t}}\)，从而控制\((P_x,P_y)\)的移动速率，从而控制End Effector向目标处移动。

则： \[ v_x = -L_1\; s1\; \dot{\theta_1} - L_2\; s12\; (\dot{\theta_1} + \dot{\theta_2}) \\ v_y = L_1\; c1\; \dot{\theta_1} + L_2\; c12\; (\dot{\theta_1} + \dot{\theta_2}) \] 即： \[ \begin{bmatrix} v_x \\ v_y \end{bmatrix} = \begin{bmatrix} -L_1\; s1 - L_2\; s12 & -L_2\; s12 \\ L_1\; c1 + L_2\; c12 & L_2\; c12 \end{bmatrix} \begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix} \]

这个\(\begin{bmatrix}-L_1\; s1 - L_2\; s12 & -L_2\; s12 \\ L_1\; c1 + L_2\; c12 & L_2\; c12 \end{bmatrix}\)便叫做Jacobian Matrix \(J(\theta)\)，Jacobian Matrix是向量对向量的一阶导。

根据上述公式，让我们思考一下：若\(\begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix}\)持续固定值不变，则\(\begin{bmatrix} v_x \\ v_y \end{bmatrix}\)是否也会持续固定值不变，进而让End Effector沿着一个固定的方向一直运动下去呢？答案是否定的。因为虽然\(\begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix}\)固定不变，但\(\begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix}\)反映的是\((\theta_1,\theta_2)\)的变化率，前者只要非0，则在时间轴上，\((\theta_1,\theta_2)\)会变，\(J(\theta)\)跟着变，导致\(\begin{bmatrix} v_x \\ v_y \end{bmatrix}\)也变。而且一看图便知道，end effector有一个运动的范围，不会沿着一个方向不断运动下去。经过上述的思考，我们很容易想到，end effector的运动范围跟\(J(\theta)\)的性质有关。

那么，我们是否可以根据\(J(\theta)\)推测出end effector的运动边界？(一个半径为\(L_1+L_2\)的圆)我无法回答这个问题，因为我觉得\(J(\theta)\)是不断变化的，没有一个固定的值；没有一个固定的值，我暂时还没想到怎么算出\((L_1+L_2)\)的运动半径来。

但我觉得，可以回答这么一个问题：在什么情况下，end effector会到达它的运动边界？我仍然没想到如何单纯从\(J(\theta)\)的形式上推导出答案，但显而易见的是，我们一看图，就知道当\(\theta_2 = 0\)时，机械臂伸直了，end effector会运动到它的边界。此时\(J(\theta)\)刚好是奇异的，也就是\(det(J(\theta))\)的值为0，也就是\(J(\theta)\)的\(col_1\)和\(col_2\)向量的方向是重合的，且刚好与此时机械臂伸直的方向是相切的，即\(\begin{bmatrix} s1 \\ c1 \end{bmatrix}\)。

当前系统这个

机械臂伸直,end effector到达它的运动边界
\(\theta_2 = 0\).
\(J(\theta)\)为奇异阵

的状态，我暂且给它取一个名字，叫做“奇异态”。表面上来看，因为\(J(\theta)\)已经是奇异的了，两个列向量已经线性相关了，无论右乘向量\(\begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix}\)如何变化，\(J(\theta)\)都会是奇异阵，系统都处于“奇异态”，但我们上文已经说过了\(\begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix}\)只要非0，则随着时间t流逝，它会引起\(J(\theta)\)的变化，从而会破坏系统的“奇异态”。但其实，仅仅要\(\begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix}\)非0还不足以破坏奇异态，因为假若\(\dot{\theta_2}=0\)，即\(\theta_2\equiv 0\)，此时 \[ \begin{bmatrix} -L_1\; s1 - L_2\; s12 \\ L_1\; c1 + L_2\; c12 \end{bmatrix} \equiv \frac{L_1+L_2}{L_2} \begin{bmatrix} -L_2\; s12 \\ L_2\; c12 \end{bmatrix} \] \(J(\theta)\)恒为奇异阵，系统恒为“奇异态”，end effector将绕原点做半径为\(L_1+L_2\)的圆周运动，运动方向为\(J(\theta)\)的列向量相同，即与\(\theta_1\)相切。

Planning using inverse kinematics

(EX1 begin)

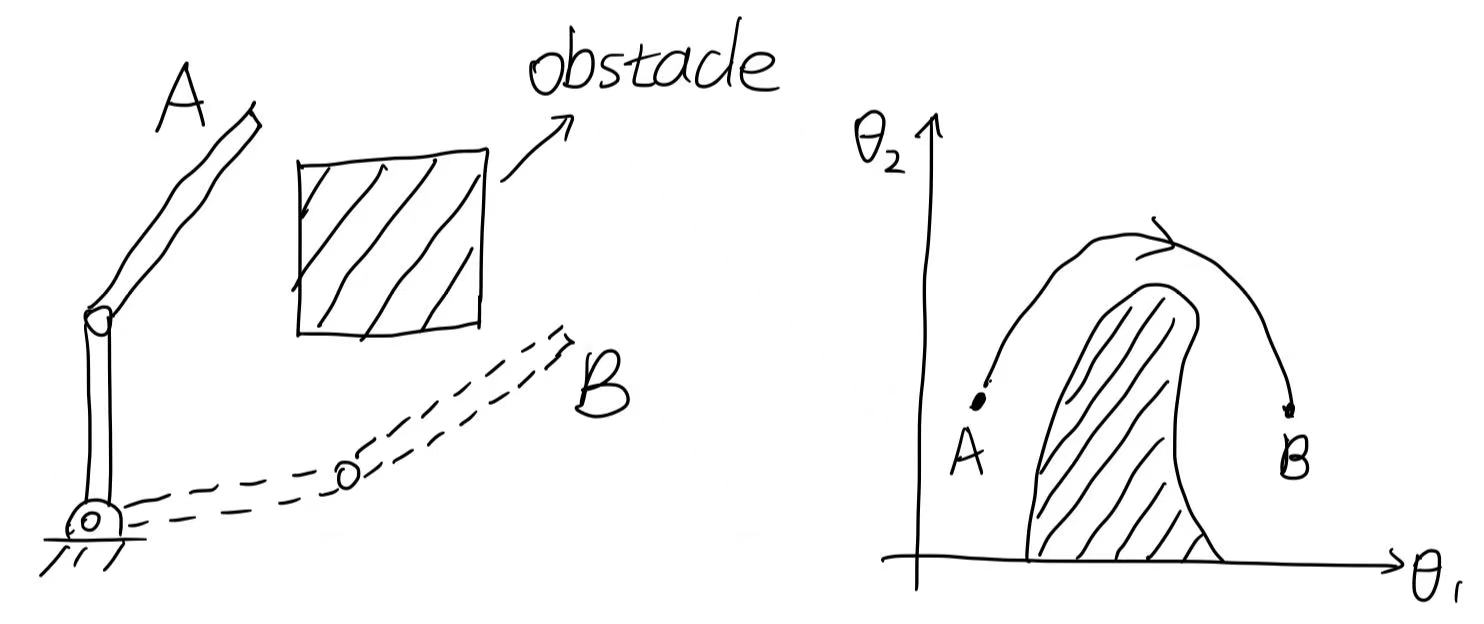
planning_intro

(EX1 end)

Control

(EX1 begin)

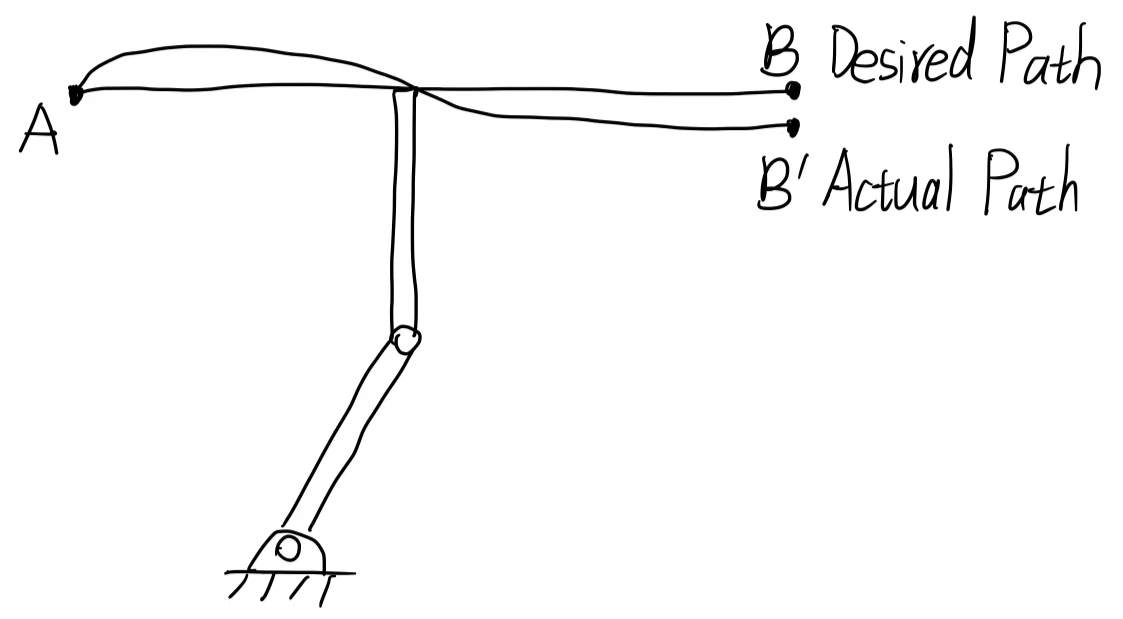
control_intro

(EX1 end)

在上例中，desired path与actual path之间的误差就是control要解决的问题。引起误差的原因可能有：

noise, disturbance
kinematic parameter errors (比如我设计了一根杆子长1m，但制造出来后却长1.1m)
modeling errors
friction, elasticity, backlash
other unmodeled errors

如何解决这些问题呢？就要用到feedback control

MOBILITY (DEGREE of FREEDOM)

Intro to DoF

如何认识自由度？先举个例子：在桌子上唯一确定一个硬币的位置。

(EX1 begin)

Where is the coin? How to uniquely determine its position?

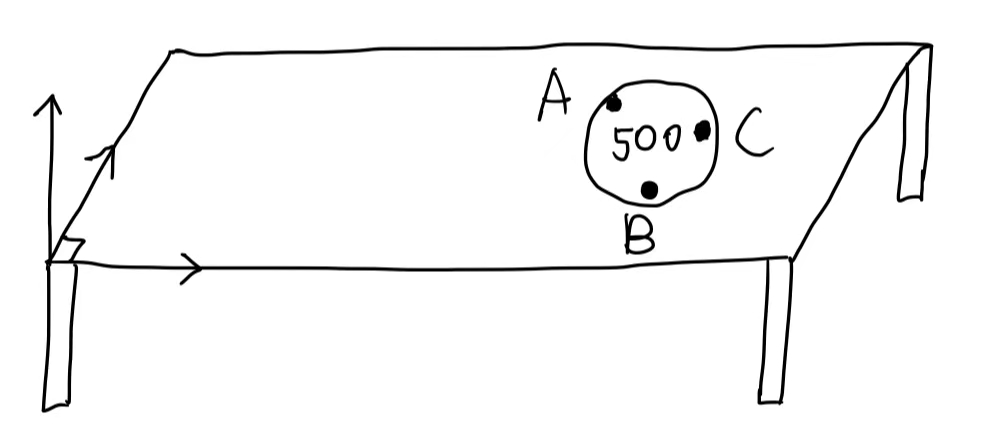
where_is_the_coin

Solution 1, step by step:

选取一个参考系(图中已画出，左下桌角处)
在硬币上选取若干个点。只需要3个就够了，{A, B, C}。但对于这3个点，我们要设一定的限制，即两两点之间的距离(\(L_2\)范数)固定为{\(L_1, L_2, L_3\)}。即： \[ d(A, B)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}=L_1 (fixed) \\ d(B, C)=\sqrt{(x_B-x_C)^2+(y_B-y_C)^2}=L_2 (fixed) \\ d(A, C)=\sqrt{(x_A-x_C)^2+(y_A-y_C)^2}=L_3 (fixed) \] 于是，我们有了3个等式，包含6个未知数。也就是说，我们要唯一确定该硬币在桌子上的位置，需要确定3个自由变量(6-3=3)。也就是说，唯一确定硬币在桌子上位置的参数里，有3个独立变量。
也就是说，如果(\(x_A, y_A\)), \(x_B\)被给定了，我们就可以算出\(y_B\), (\(x_C, y_C\))来。如下图所示：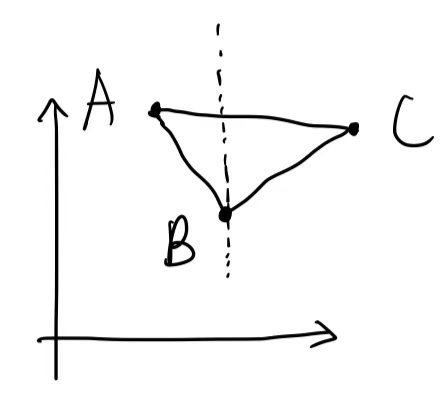

但实际上，上图只是理想情况，其实还有这里应该有两种解：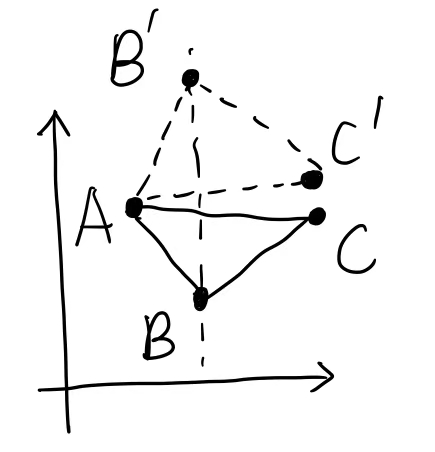

针对这种两种解的情景，我们用”reflection(反射)”去描述它，即上图中上下两个解互为镜像。所以在桌面上唯一确定coin的位置的时候，我们必须限定反射是不被允许的，我们必须舍弃掉”top-solution”。

Solution 2:

然而，上述的方法终究不够优美，我们有另一种更优美的办法来唯一确定桌面上的硬币位置：

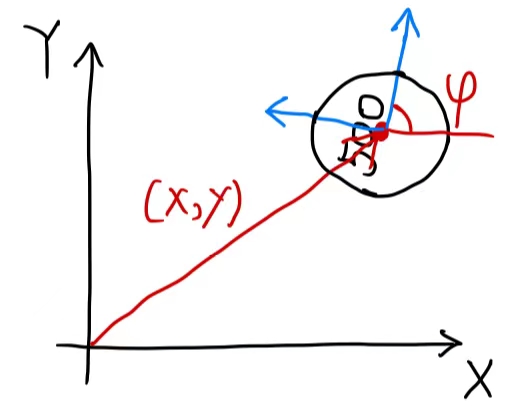
DoF_coin_TR

(EX1 end)

上述的EX1考虑的是2D空间中刚体的自由度，现在我们考虑在3D空间中刚体的自由度。

(EX2 begin)

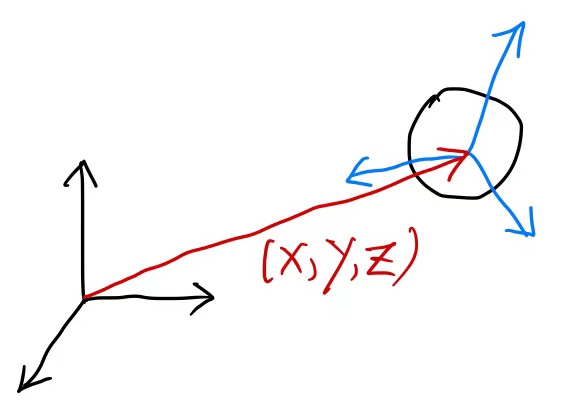
DoF_coin_3D

假设上图中3D空间中的问题还是一个coin，我们还是要唯一确定它在3D空间中的位置，则对于上图而言，硬币质心的位移参数我们已经知道: (x, y, z)，那我们该如何确定硬币的朝向呢？也就是问，除了确定位移的3个参数外，我们该用多少个参数才能确定硬币的朝向呢？

我们仍然还是先按照Solution 1的方式来做，先在硬币上确定3个点，如图：

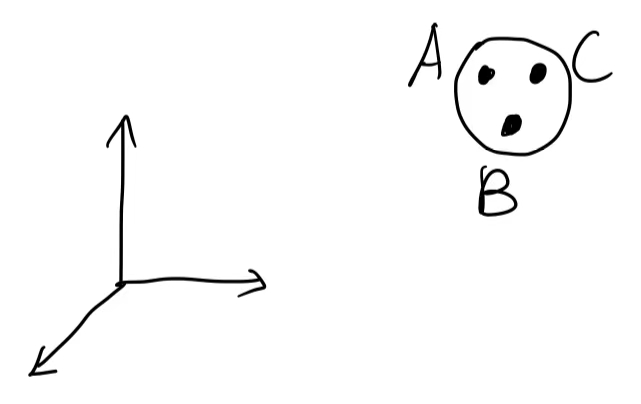
three_points_coin_3D

则有等式： \[ d(A, B)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}=L_1 (fixed) \\ d(B, C)=\sqrt{(x_B-x_C)^2+(y_B-y_C)^2+(z_B-z_C)^2}=L_2 (fixed) \\ d(A, C)=\sqrt{(x_A-x_C)^2+(y_A-y_C)^2+(z_A-z_C)^2}=L_3 (fixed) \] 其中有3个等式，9个未知数，即6个自由/独立参数(9-3=6)，而确定硬币位移用了3个参数，所以确定转向还需要用3个参数。

(EX2 end)

Mobility of Robot Mechanisms

现在介绍较复杂的机器人机械结构的DoF的计算。

首先介绍一些常见关节：

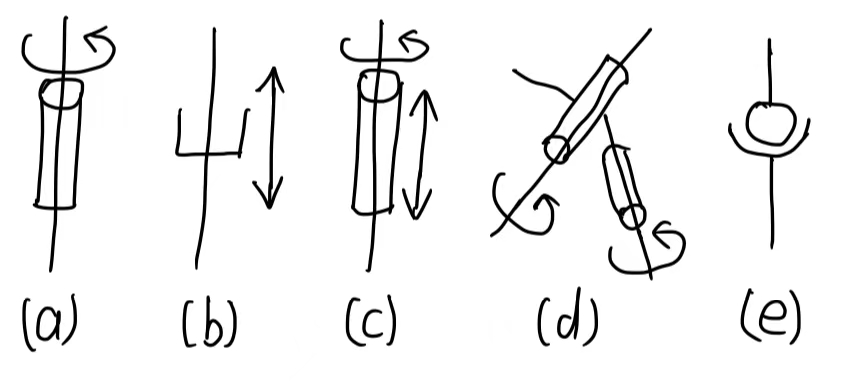
common_joints

从左到右依次是：

Revolute (R) joint, DoF=1
Prismatic (P) joint, DoF=1
Cylinderical (C) joint, DoF=2
Universal (U) joint, DoF=2
Spherical (S) joint, DoF=3

Planar Robot

现在我们来考虑一个平面上的机器人，假设下图中椭圆形的是足：

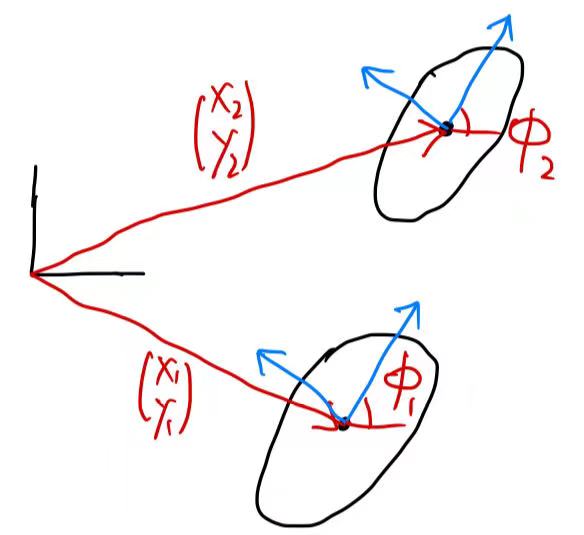
如果只考虑一条腿，则它的DoF=3

考虑两条腿的话，DoF=6
如果两条腿被用R关节铰接在一起：

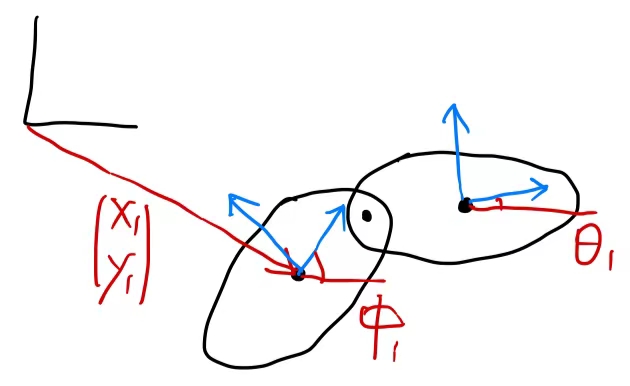
则DoF=4
如果三条腿被用R关节铰接在一起：

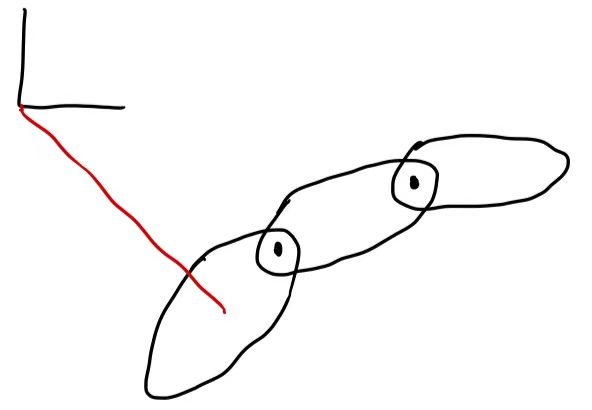
则DoF=5，(\(x_1, y_1, \Phi_1, \Theta_1, \Theta_2\))
上述3张Planar robot的铰接用的都是DoF=1的R关节，假如我们用DoF=2的R+P联合关节呢？如下：

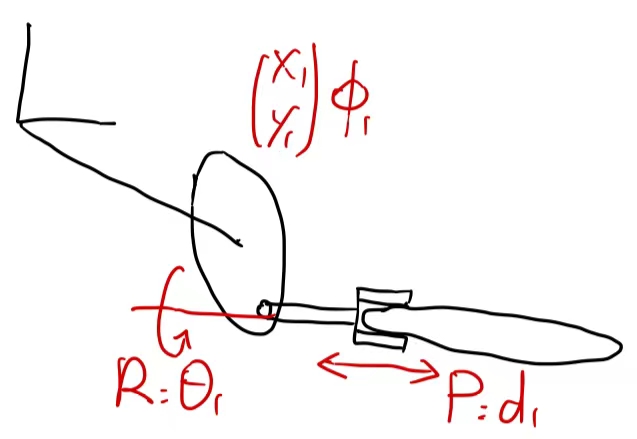
则DoF=5，(\(x_1, y_1, \Phi_1, \Theta_1, d_1\))

由上述例子，其实我们可以总结出一个计算DoF的公式，即Gruebler Formula (Planar Version): \[ N = \#~of~links~(including~ground) \\ J = \#~of~joints \\ f_i = DoF~of~joint~i,~i=1,…,J \\ DoF=3 (N-1) - \sum_{i=1}^{J} (3-f_i) = 3 (N-1-J) + \sum_{i=1}^{J} f_i \]

(EX1 begin)

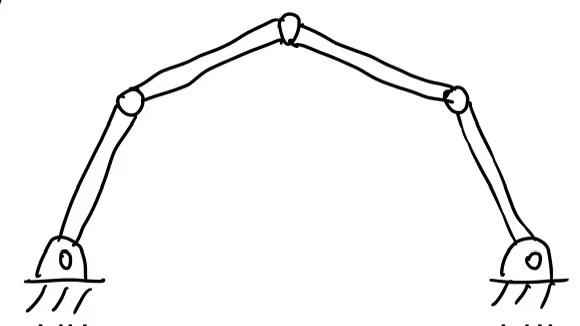
dof_ex_1

DoF=3*(5-1-5)+5=2

这意味着如果我们固定住其中两个关节点，则整个结构都会被固定住

(EX1 end)

(EX2 begin)

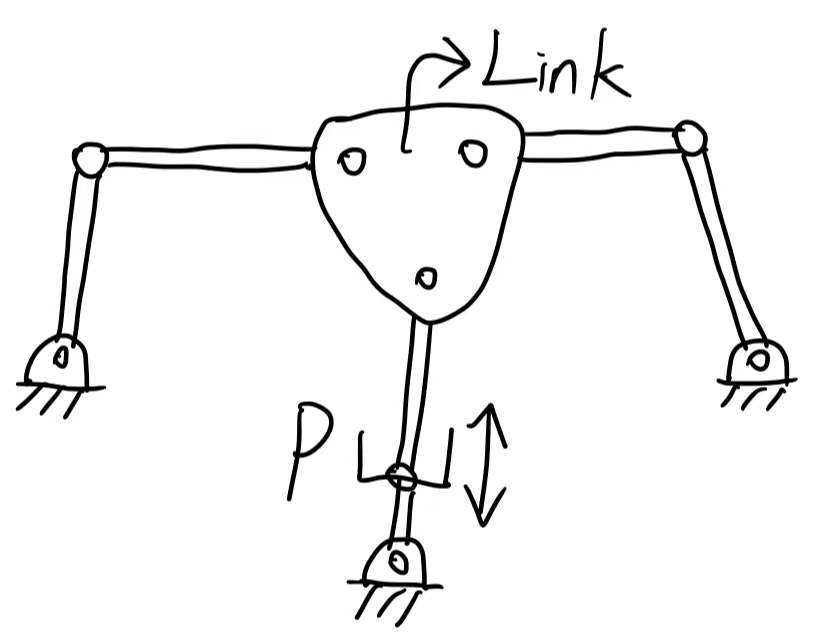
dof_ex_2

N=8, J=9

DoF=3*(8-1-9)+9=3

(EX2 end)

(EX3 begin)

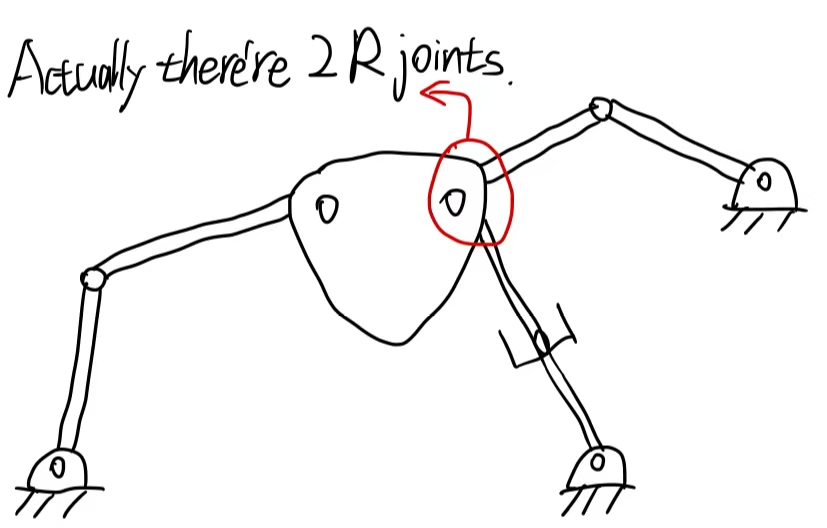
dof_ex_3

每个关节链接且仅链接两个Links/Bodies! 然而，每个Link可以链接超过两个关节。

DoF=3

(EX3 end)

(EX4 begin)

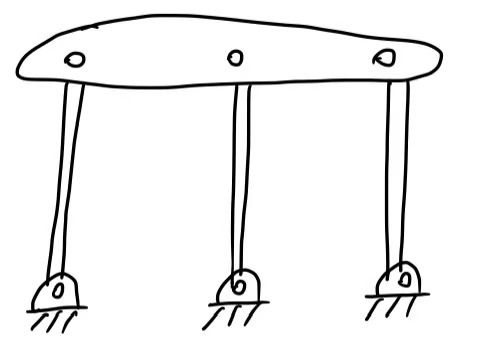
dof_ex_4_v1

N=5, J=6, \(j_i\)=1

DoF=3*(5-1-6)+6=0

它居然不能移动！但是我们明显看上去这个结构是可以移动的啊？难道Gluebler公式出错了？是的，对于Gluebler公式来说，的确存在一些例外情况。但是在大多数情况下，Gluebler是正确的。例如，如果上述机械结构的3根Link不是等长的， Gluebler公式将会十分稳健，如下图所示，这个结构就是不能移动：

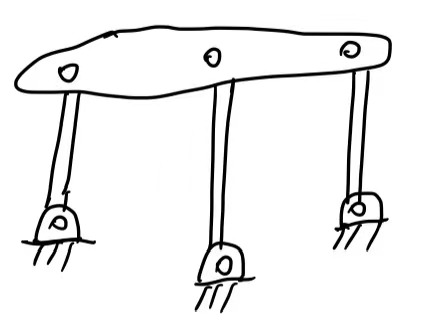
dof_ex_4_v2

事实上，该结构中，3根link完全等长的情况在现实世界中是不存在的，所以从这种意义上来讲，Gluebler仍然是正确无误的。

(EX4 end)

Spatial Mechanism

对于3D空间中的Spatial Mechanism而言，同样有Spatial Version的Gluebler Formula: \[ DoF=6\dot (N-1)-\sum_{i=1}^J (6-f_i) = 6\dot (N-1-J)+\sum_{i=1}^J f_i \]

(EX1 begin) 这是一个6*UPS platform

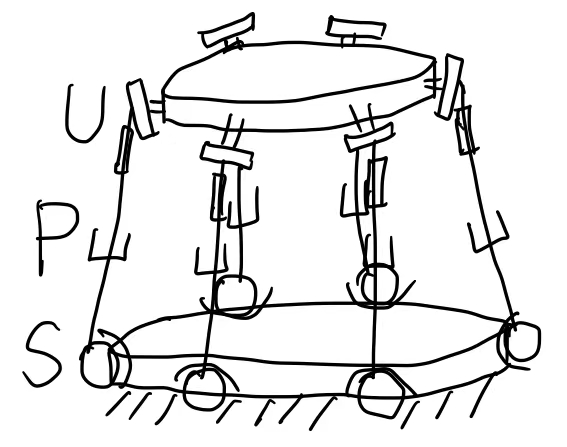
dof_ex_3D_1

DoF=6(14-1+18)+6(3+2+1)=6

(EX1 end)

(EX2 begin) 这是一个3*UPS platform

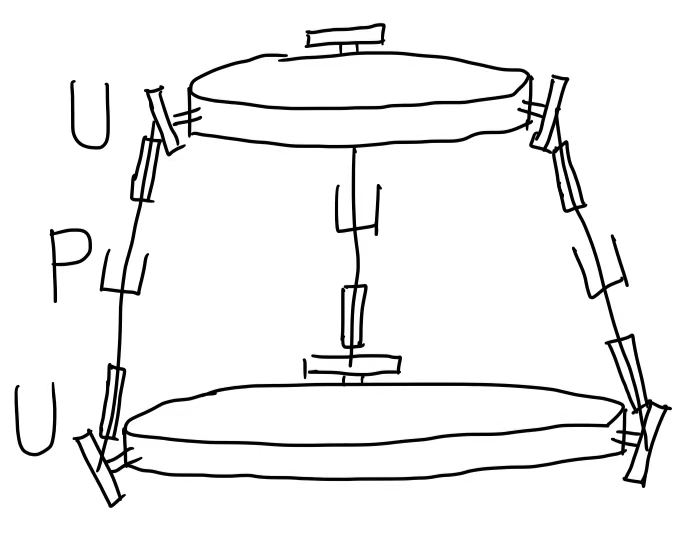
dof_ex_3D_2

DoF=6(8-1-9)+35=3

“所以对于这个例子而言，你可以仅仅在3个Prismatic Joints处放置3个电机，就能控制整个平台的升降。并且如果你固定住任意3个joints，整个平台都动不了。”

“”里的说法看上去很对，但实际上是错的，因为DoF实际上不是3。没错，Gluebler又失效了。DoF实际上是5。上例中的机械结构实际上是一个奇异(singular)的机械结构，奇异的机械结构的DoF比Gluebler所计算的要多。

这种奇异(singular)的机械结构将会在讲close chain时详细论述。

(EX2 end)

Another Way to Understand Mobility (DoF)

上述通过几个例子从几何角度去理解自由度，并从中总结出了Glubler Formula。

其实还有另一种从代数角度理解DoF的方式。这种方式暂时不涉及到Glubler Formula。

下面也举几个例子说明这种理解方式。

(EX1 begin)

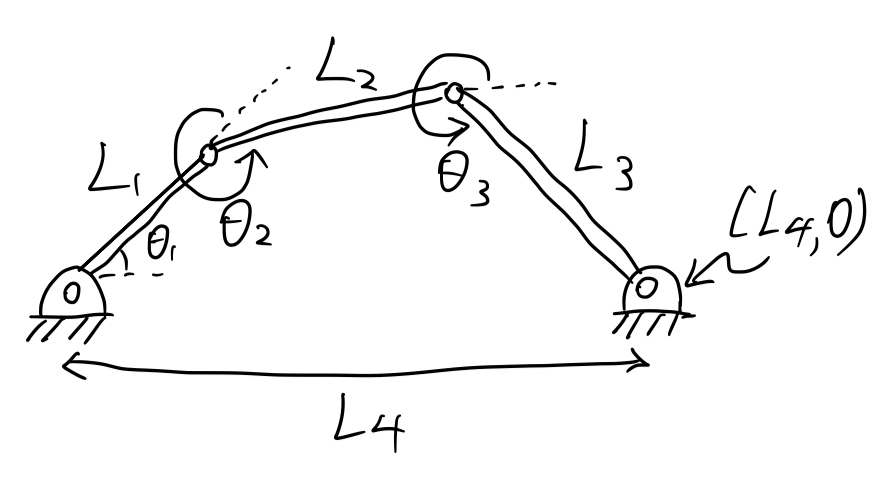
New_way_understand_DoF_ex1

考虑到本例，这是一个平面上的3关节的 open chain，并且末端被固定在\((L_4, 0)\)。

就此，我们可以列出下列等式，以确定整个系统的状态：

\[ L_1 cos(\theta_1) + L_2 cos(\theta_1 + \theta_2) + L_3 cos(\theta_1 + \theta_2 + \theta_3)=L_4 \\ L_1 sin(\theta_1) + L_2 sin(\theta_1 + \theta_2) + L_3 sin(\theta_1 + \theta_2 + \theta_3)=0 \]

上述有2个等式，3个未知数，于是我们从线性代数的角度出发，可以说：“上述线性方程组有1个自由度，只要我们确定1个未知数的值，其他2个未知数也随之确定。也就是说，我们固定一个关节的角度，整个系统都会被固定住。于是系统的自由度是1。”

于是，我们可以直觉得出，上述线性方程组的可行解在其解空间中是一条线：

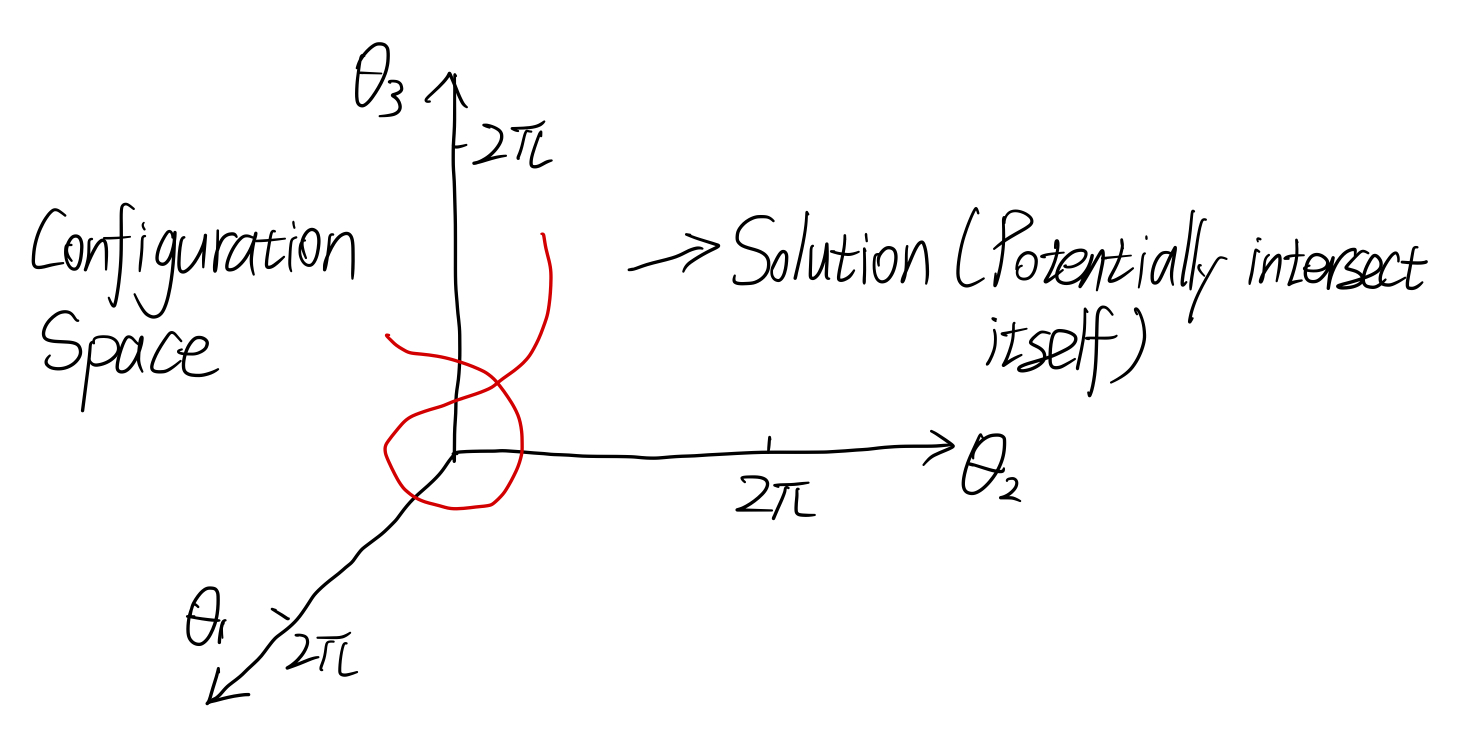
New_way_understand_DoF_ex1_solution

(EX1 end)

(EX2 begin)

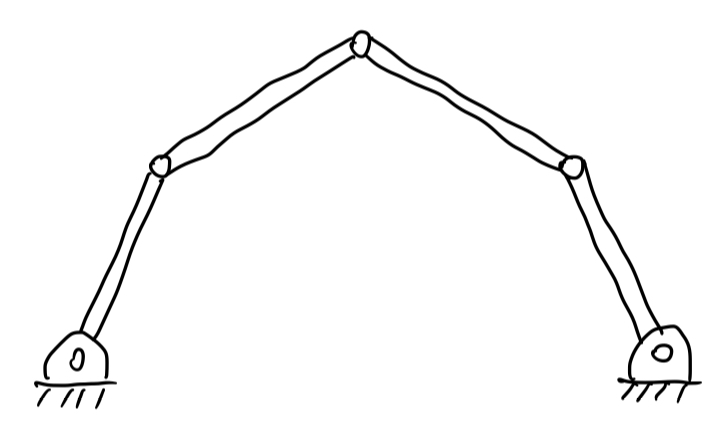
New_way_understand_DoF_ex2

又如对于此例EX2，如同EX1，你可以列出一个线性方程组来描述系统的状态，并且该方程组中有2个等式，4个未知数，于是系统DoF=2。

于是，我们可以直觉得出，此线性方程组的可行解在其解空间中是一个平面：

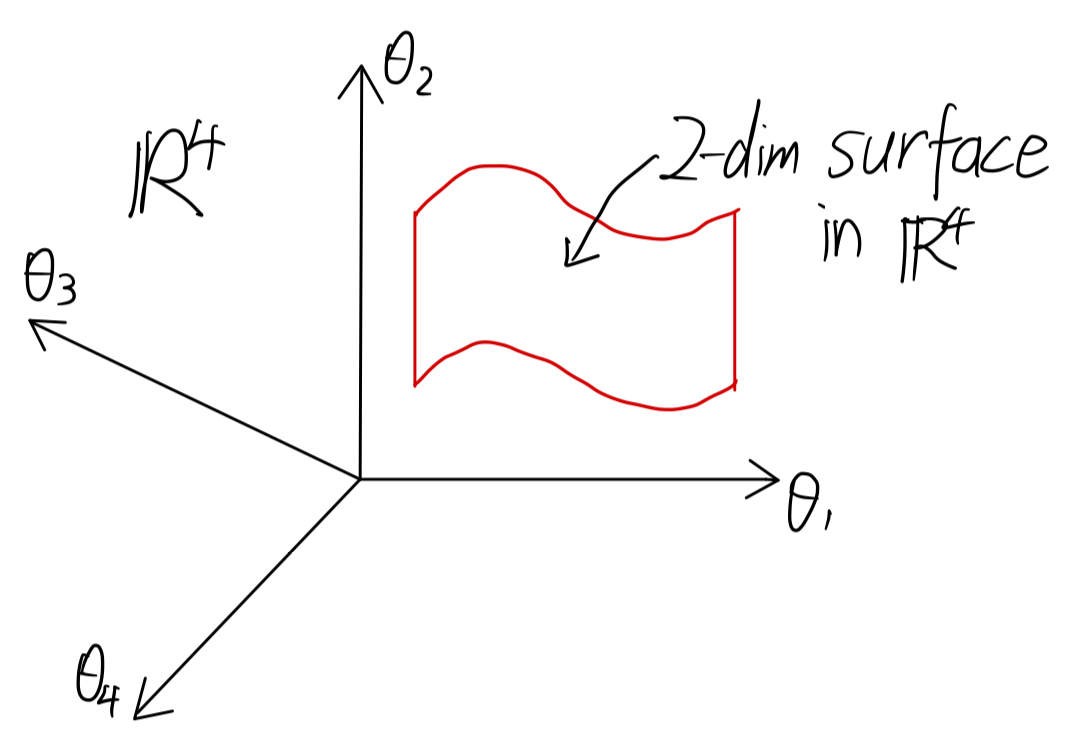
New_way_understand_DoF_ex2_solution

(EX2 end)

PLANAR GRASPING

Form and Force Closure

Introduce

这一节，我们引入 Form Closure 和 Force Closure 的概念。

在详细讲述这两个概念之前，我们线提两个 Motivating Example:

(EX1 begin)

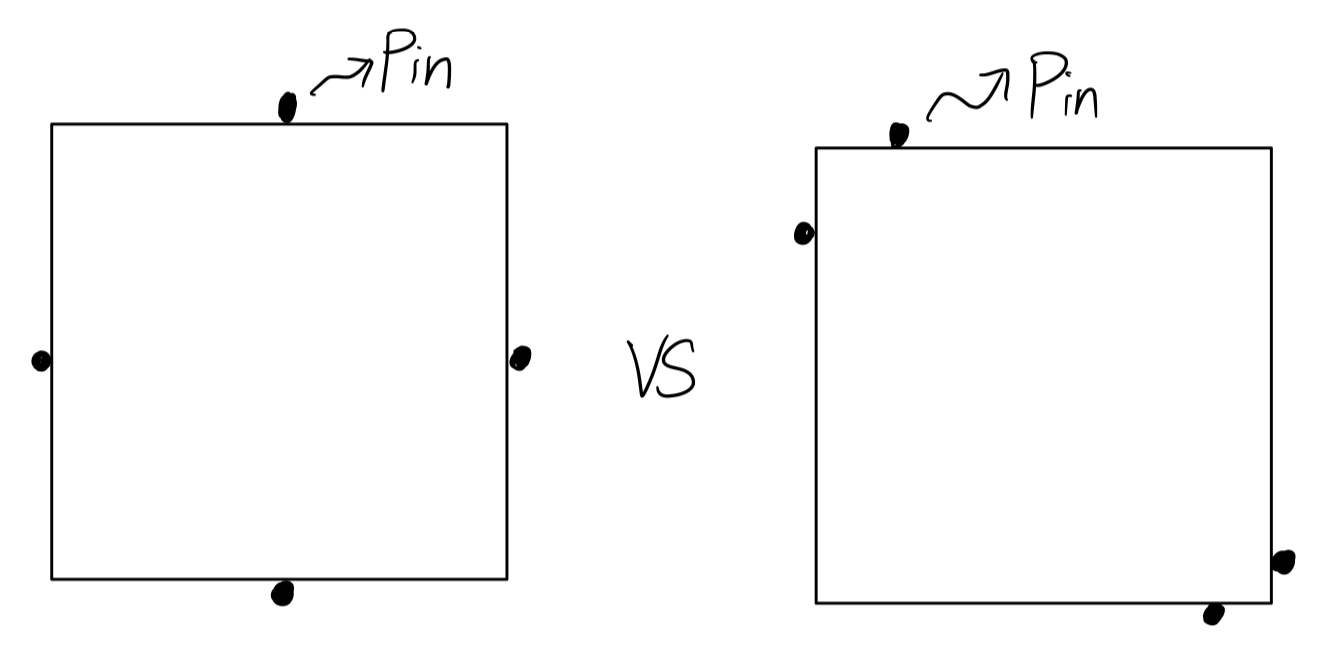
form_force_closure_intro_ex1

上图中的pins是无摩擦力的点接触 (frictionless point contacts)，也就是抓取物体的接触点，但我们假设这里不存在摩擦力。请问，上图中，左边和右边两种抓取方式，哪种更好？

其实是右边的更好。

为什么？我们下文会解释到。

(EX1 end)

(EX2 begin)

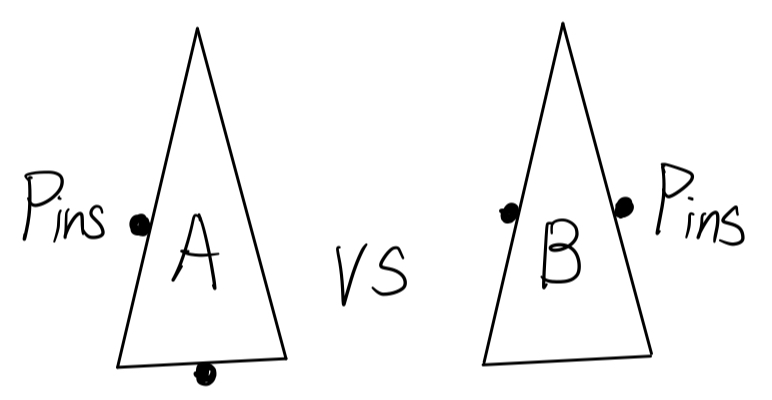
form_force_closure_intro_ex2

在这个例子中，我们假设 pins 是有摩擦力的。那么上图中左右两边哪种抓取方式更好？

还是右边的那种。我们在后面会揭开原因。

(EX2 end)

为了衔接上下文的教程，我们这里具体定义一下 Form Closure 和Force Closure：

Form Closure：An object is completely immobilized by a set of point contacts.
Force Closure：Fingers can apply forces to resist any external forces on object.

这里要额外注释一下：

Form Closure指的是通过机械结构本身的几何形状来固定物体，使得物体无法在任何方向上移动或旋转。在Form Closure的情况下，物体被完全“锁定”，不依赖于抓取力的大小或方向。Form Closure的一个典型例子是将一个石块放入一个精确匹配的凹槽中，石块无法从凹槽中移动除非改变整个结构。参照EX1
Force Closure则是指通过施加外力（如抓取力）来固定物体，即通过力的作用使物体在受力状态下无法移动。这种方式依赖于施加的力的大小和方向，以及力的分布是否能够平衡物体可能产生的任何运动。在Force Closure的情况下，即使物体的外形和抓取器不完全匹配，只要抓取器能施加足够的力，也能有效地固定物体。一个例子是用手抓住一个球：虽然球和手的形状不完全匹配，但通过手对球施加的压力，球可以被固定住。参照EX2

而在非理想现实中，我们遇到的实际情况都是Force Closure，于是Force Closure才是最重要的。所以下面的所有例子我们并不额外说明的话，都是只考虑Force Closure，也就是明知force的存在。但需要注意的时，有些时候，我们只考虑normal force的存在而假设friction不存在，关于这点详见下面“Contact Types”一节。

Contact Models

这里我们对Force Closure场景中 pins 与物体的接触做一个接触建模，以准确地描述Force Closure中的接触。

接触模型即如下图：

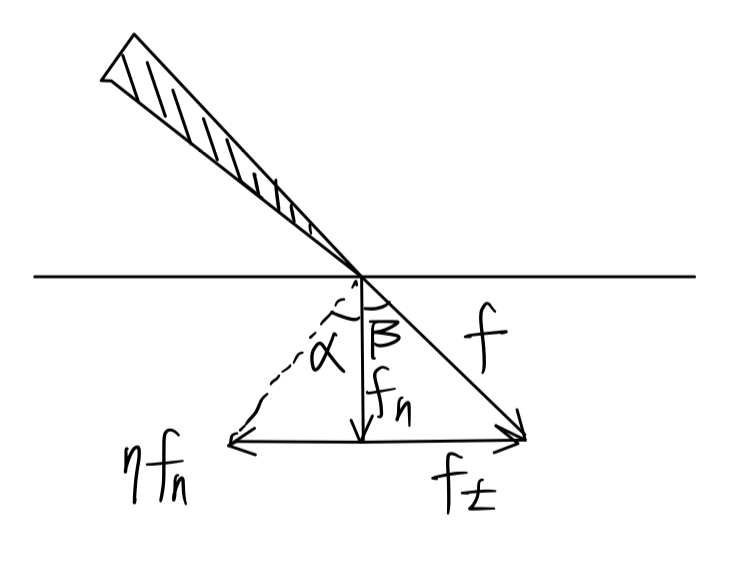
contact_model_friction

上图中，楔子就是Pin，它与物体接触。

这个接触看上去随时要滑动(slipping)一样，我们不希望它滑动。那么，滑动什么时候发生呢？答案是 \(\vert f_t \vert > \eta \vert f_n \vert\)。\(\eta\)是什么？\(\eta\)是Coulomb Friction Coefficient。

也就是说，滑动发生的充要条件是：\(\alpha < \beta,\; \alpha = tan^{-1} \mu\)

为了简化上述关于“滑动发生的充要条件”的表述，我们在接触模型，引入一个Friction Cone的概念：

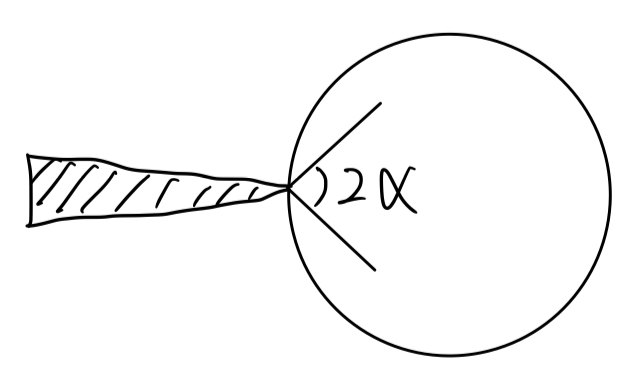
contact_model_friction_cone

于是，滑动发生的充要条件是：Force is Outside the Friction Cone.

Contact Types

Contact可以被分为两类：

Frictionless Point Contact:
- \(\alpha = 0\) or \(\eta = 0\)
- Only normal force can be applied
Point Contact with Friction
- Force can only be applied inside the friction cone.

Static Equilibrium

一个物体受到外力(External Force, eg. grivaty)的影响，会移动，于是我们用手指去抓稳它，也就是让它静止(Stationary/Immobilized)，于是手指就施加一群力到该物体上。

要是这时候物体静止了，我们就说物体达到了Static Equilibrium。

Static Equilibrium有没有数学上的描述？详见下面的例子：

(EX1 begin)

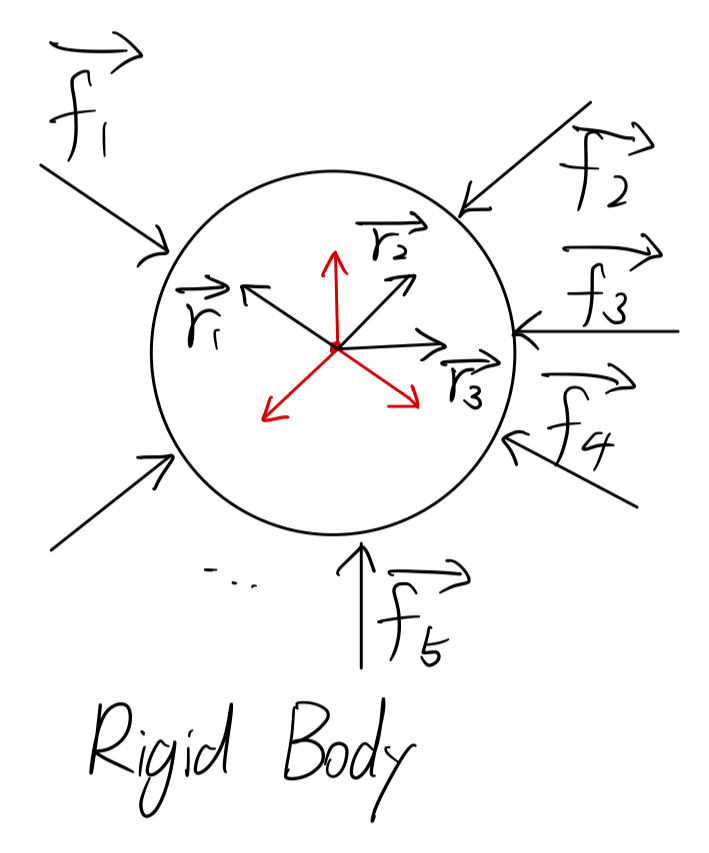
contact_equilibrium_ex1

在这个例子中，我们假设不存在friction，于是所有接触都是frictionless contact，所有力都是normal force。

同时，在这个例子中，我们不定义外力External Force。

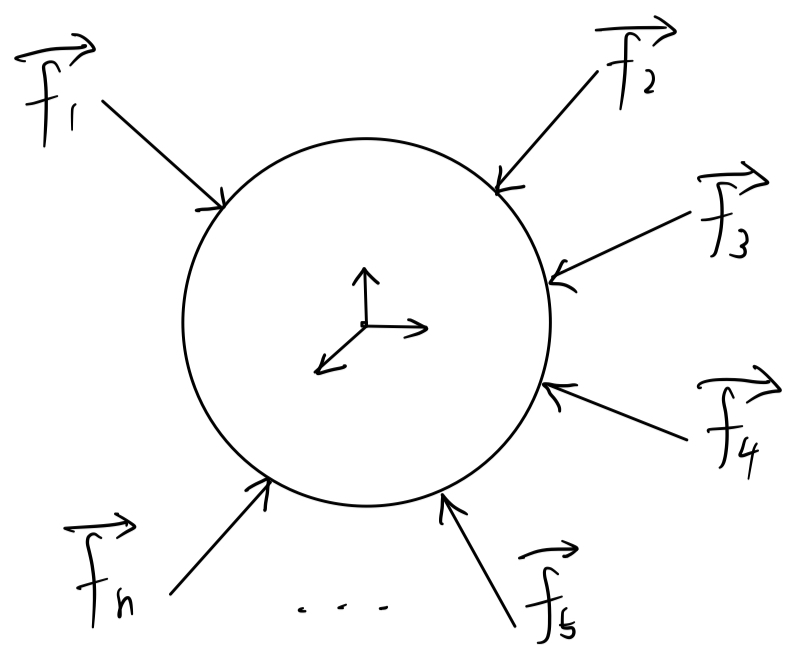
从高中知识来看，什么情况下该物体会静止？“大小相等方向相反”对吗？也就是\(\sum \vec{f_i}=0\)对吗？但这是不够的，因为高中阶段我们往往把受力平衡的问题简化为了质点。但当物体不是质点时，仅仅用上述公式去约束force，可能物体的确不会移动，但还是会旋转，看下图你就明白了：

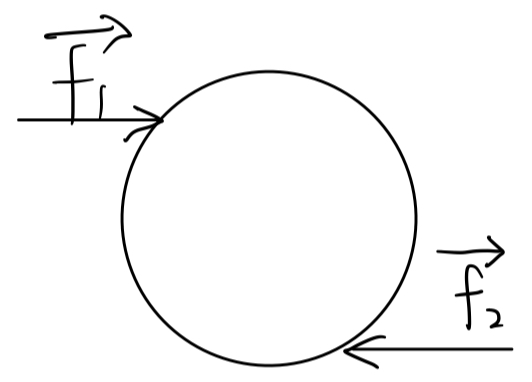
contact_equilibrium_ex1_rotate

对于这张图而言，两个force中的任一个都会使得该物体顺时针旋转。而你能观察到的一个有趣的现象时，当只分析平面上的受力时，若一个力使得物体顺时针旋转，则该力的力矩(moment/torque)的z分量将是负数。力矩是什么？从物体质心为起点引一个向量到受力点来，设为\(\vec{r}\)，则\(\vec{r} x \vec{f}\)即为力矩。

话归正题，为了使得本例中的问题达到Static Equilibrium，我们一共要给forces加上2条约束： \[ \sum \vec{f_i}=0 \\ \sum \vec{r_i} \times \vec{f_i}=0 \]

第一条平衡力，力之和为0防止位移。

第二条平衡力矩，力矩之和为0防止旋转。 </span>

我暂时不知道这组公式叫什么名字，我暂且称之为”Static Equilibrium 方程组”。

(EX1 end)

为了进一步深入了解分析Static Equilibrium 方程组，我们将上述EX1简化成下面的EX2，并分析：

(EX2 begin)

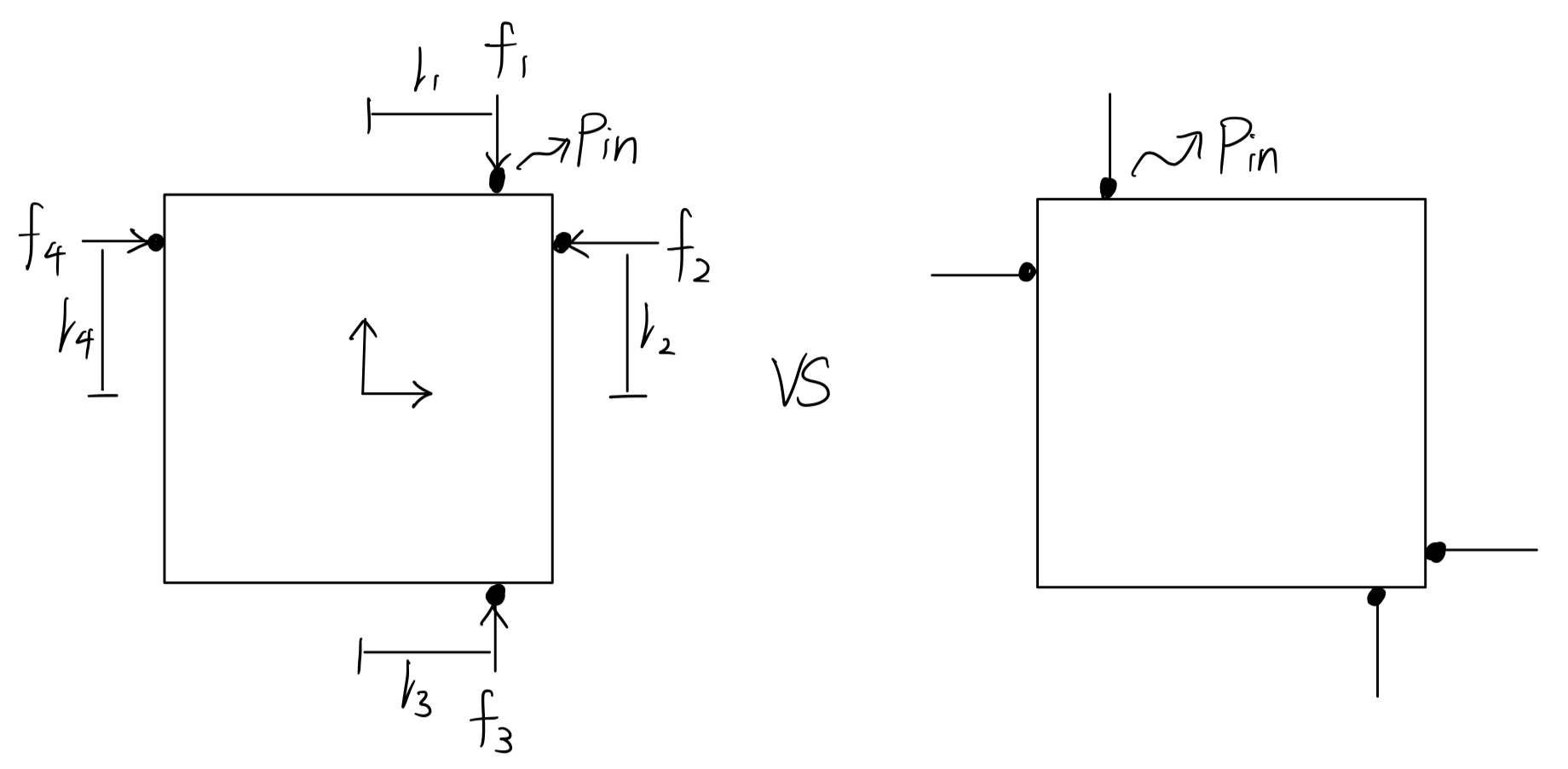
contact_equilibrium_ex2

在这个例子中，我们仍然假设不存在friction，于是所有接触都是frictionless contact，所有力都是normal force。

在这个例子中，假设外力External Force被引入了，则物体仅在下列式子成立时达到static equilibrium：

\[ \sum_{i=1}^n \vec{f_i}+\vec{f_{ext}}=0 \\ \sum_{i=1}^n (\vec{r_i} \times \vec{f_i}) + \vec{r_{ext}} \times \vec{f_{ext}}=0 \]

在本例中，n=4，且： \(f_1 = \begin{bmatrix} 0 \\ -x_1 \end{bmatrix}\), \(f_2 = \begin{bmatrix} -x_2 \\ 0 \end{bmatrix}\), \(f_3 = \begin{bmatrix} 0 \\ x_3 \end{bmatrix}\), \(f_4 = \begin{bmatrix} x_4 \\ 0 \end{bmatrix}\)。

并且，我们约束\(x_i \geq 0\)，这意味着force只能推(push)，不能拉(pull)。这种约束想想也是合理的，毕竟每个force都可视作于一根手指按在物体上，你指尖按上去了肯定只能给到压力啊，肯定只能推啊，拉不了。

对于Static Equilibrium方程组第一式，在本例中可以具体为： \[ \begin{bmatrix} -x_2+x_4+f_{ext,x} \\ -x_1+x_3+f_{ext,y} \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \end{bmatrix} \]

对于Static Equilibrium方程组第二式，在本例中可以具体为： \[ \vec{r_1} \times \vec{f_1} = \begin{bmatrix} -l_1 \\ 0 \\ 0 \end{bmatrix} \times \begin{bmatrix} 0 \\ x_1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ -l_1 x_1 \end{bmatrix} \; , \; . \;\; . \;\; . \;\; \\ \Rightarrow \begin{bmatrix} 0 \\ 0 \\ -l_1 x_1 + l_2 x_2 + l_3 x_3 - l_4 x_4 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ -m_{ext,z} \end{bmatrix} \]

有趣的是，观察第二式中的\(-l_1 x_1 + l_2 x_2 + l_3 x_3 - l_4 x_4\)，我们可以发现，\(f_1 \& f_4\)造成了物体顺时针旋转，所以它们的符号是负的，\(f_2 \& f_3\)造成了物体逆时针旋转，所以它们是正的。

言归正传，整合一式和二式，可以得到一个\(Ax=b\)的形式：

\[ \begin{bmatrix} 0 & -1 & 0 & -1 \\ -1 & 0 & 1 & 0 \\ -l_1 & l_2 & l_3 & -l_4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} -f_{ext,x} \\ -f_{ext,y} \\ -m_{ext,z} \end{bmatrix} \]

我来注解一下上述的\(Ax=b\)式子：

为达到Static Equilibrium，需要被平衡的是“力”+“力矩”
在本例中，所有力，包括外力和手指施加的力，被分解成了沿\(x\)和\(y\)的两个分量
在本例中，由于所有力都在2D平面内，所以力矩的方向只有一个，即\(z\)轴
\(x\)代表的是手指施加给物体的每个力和力矩的大小。本例中一共4个力，故\(x\)长度为4
\(b\)代表的是手指需要对抗的外力，它分为“力”和“力矩”两部分。上面一部分(在本例中是\(-f_{ext,x},-f_{ext,y}\))是外力在\(x\)和\(y\)两个方向上的分量，代表需要被平衡的“力”。下面一部分(在本例中是\(-m_{ext,z}\))是外力的力矩，代表需要被平衡的“力矩”
\(A\)按Row也分为“力”和“力矩”两部分，上面两个Row分别代表4个手指力在\(x\)和\(y\)两个方向上的分量，下面一个Row代表4个手指力在\(z\)方向上的力矩分量。但注意，\(A\)中的数值只代表力和力矩的方向，真正决定力和力矩大小的是\(x\)
\(A\)按Column来分，每个Column都代表一个手指力在\(x\),\(y\)方向上的力分量，以及在\(z\)方向上的力矩分量。但注意，\(A\)中的数值只代表力和力矩的方向，真正决定力和力矩大小的是\(x\)
\(A\)有多少个Column，就有多少个手指在抓取

考虑\(Ax=b\)，如果对于任意\(b \in \mathbb{R}^3\)，都存在一个可行解\(x \in \mathbb{R}^4\)，那么物体就能保持静止，也就是形成Form Closure

再次提醒，对于我们这里的例子而言，\(x_i \geq 0\)

那么，当\(A\)长成什么形状时，上例可现成一个Form Closure呢？

我们先来考虑一个简化的情况，我们假设物体为质点，也就是不考虑力矩了，则\(Ax=b\)可以被简化为：

\[ \begin{bmatrix} 0 & -1 & 0 & -1 \\ -1 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} -f_{ext,x} \\ -f_{ext,y} \end{bmatrix} \]

即：

\[ x_1 \vec{a_1} + x_2 \vec{a_2} + x_3 \vec{a_3} = \vec{b} \]

对于该式，有“总是有解”和“总是无解”两种情况：

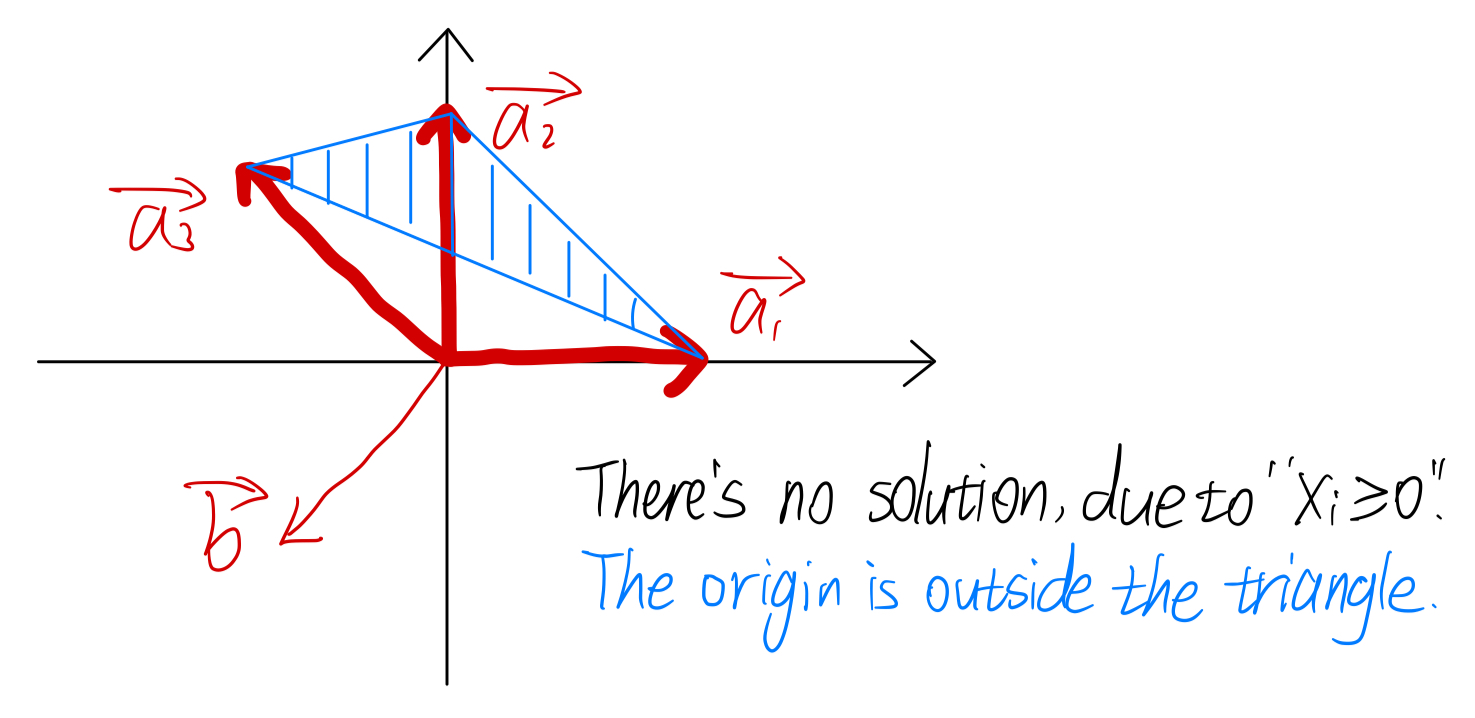
contact_equilibrium_ex2_solutable

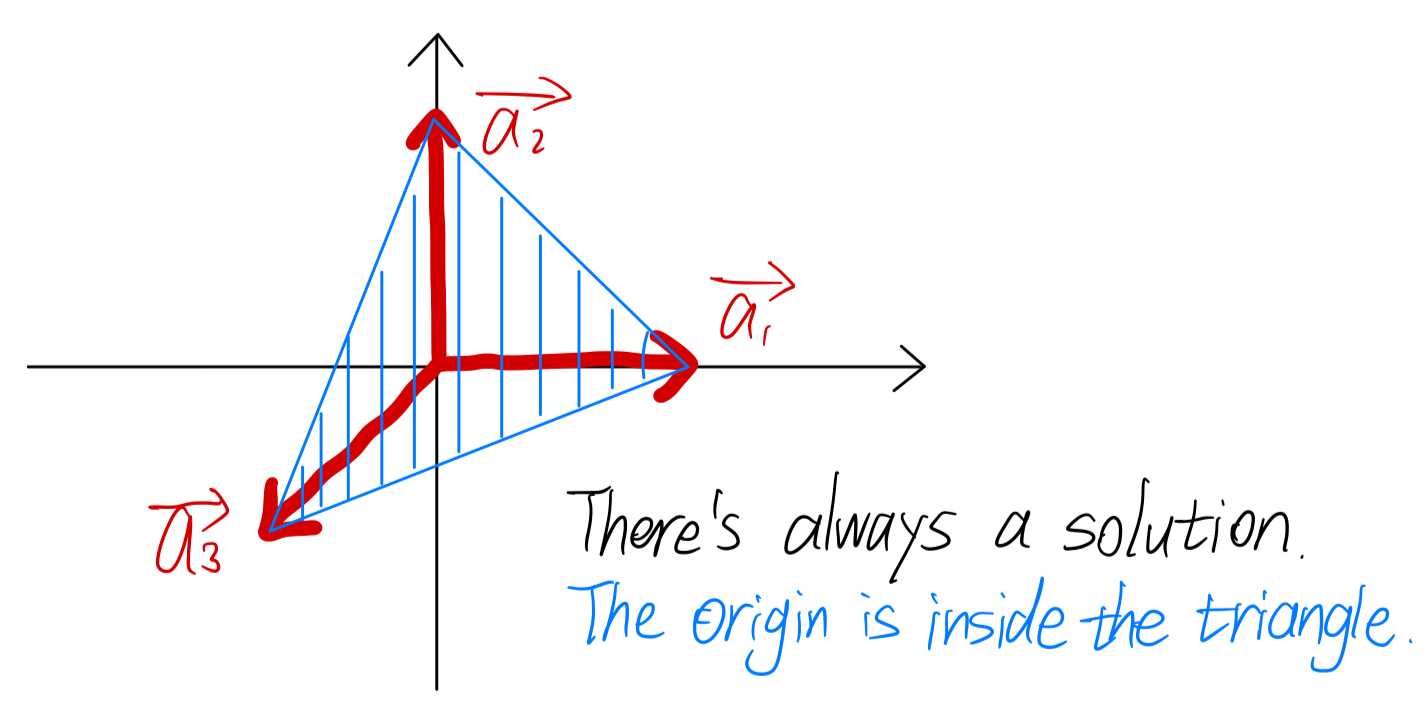
contact_equilibrium_ex2_solutionless

可以看出对于总是有解的情况而言，A的列空间的原点在列向量所现成的tetrahedron之中。换种说法是：“在\(x_i \geq 0\)的条件下，\(A\)的列向量能张成整个向量空间。”

所以对于

，A的列空间的原点也应该在列向量所现成的tetrahedron之中。既：

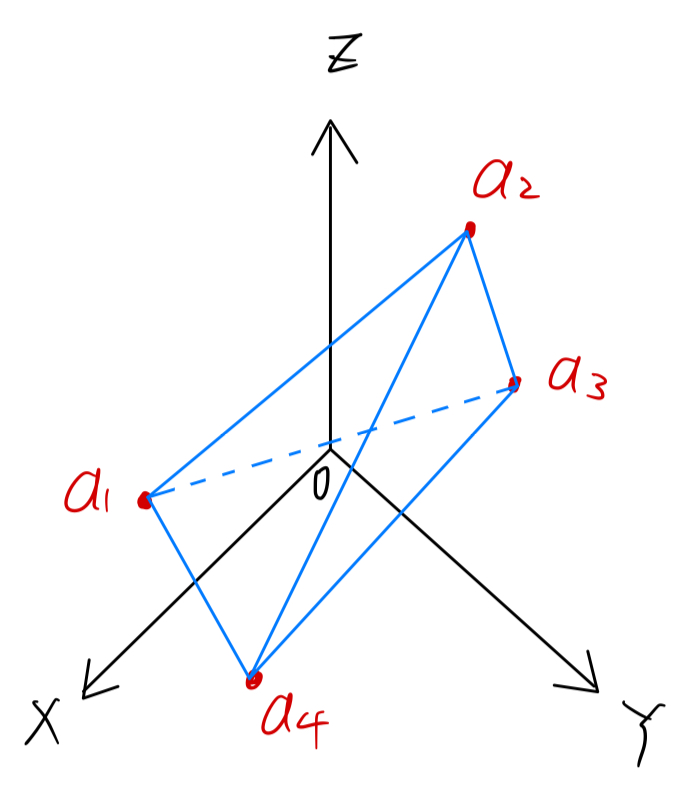
contact_equilibrium_ex2_solutable_4cols

(EX2 end)

承接上例，我们进一步假设\(l_1=l_2=l_3=l_4=0\)，则tetrahedron就会变成一个square，不再是一个tetrahedron。我们本来需要一个立体空间包住原点，但现在只剩下一个平面area。所以在这种情况下，没有解，原点不在tetrahedron中，没有Form Closure。

更具体来说，几乎没有\(b\)能在这个平面area向量空间中找到它对应的解。

事实上，这种\(l_1=l_2=l_3=l_4=0\)的情况就是下图左边这种情况：

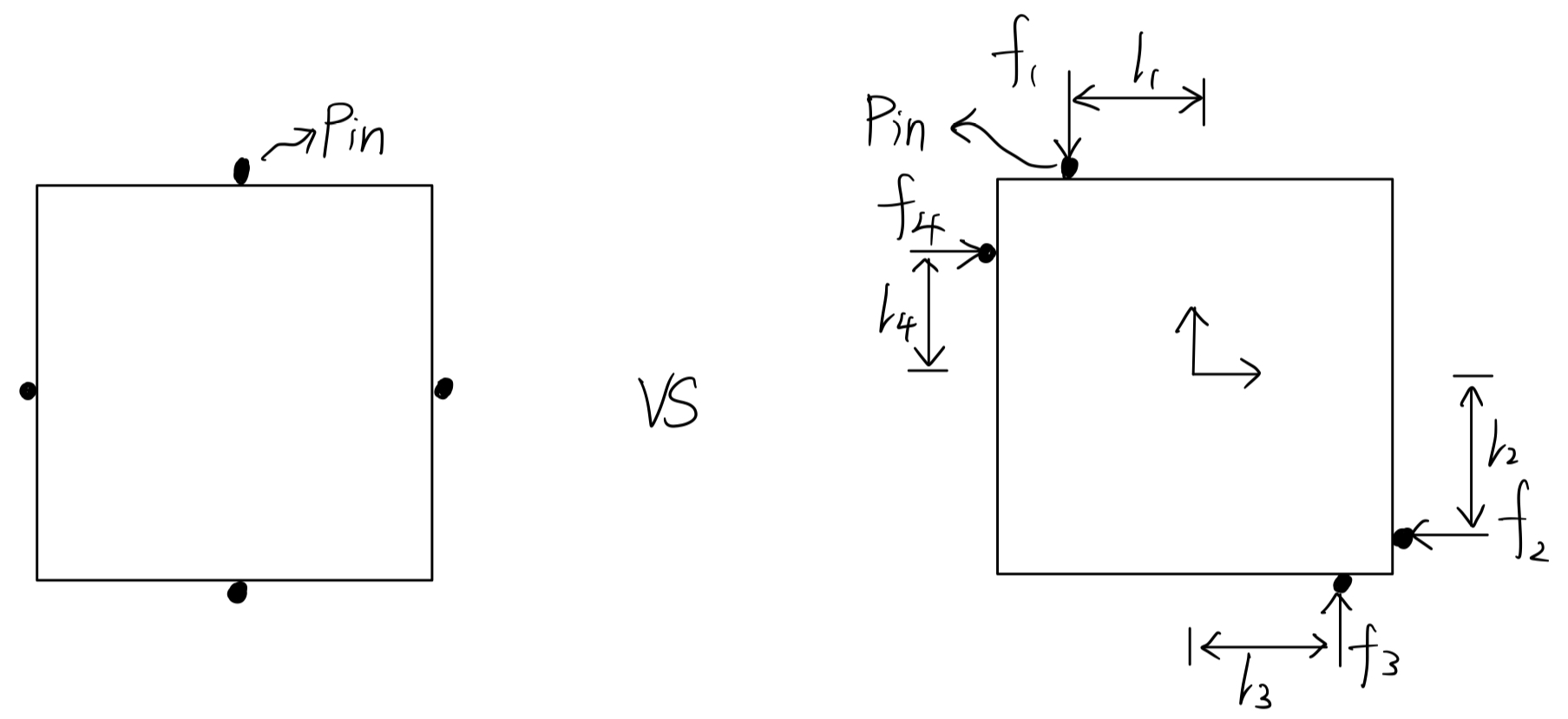
form_closure_which_better

于是我们就可以回答本章Intro小节motivating example中的问题，上图中左右两边哪一种更好？也就是哪一种更能抵抗外力？当然是右边的。

需要注意的是，上图中没有摩擦力，所以力只能朝着接触面的正交方向。并且我们简化了这里的力，它只能push，所以\(x_i \geq 0\)。也就是说对于\(f_1 = \begin{bmatrix} 0 \\ -x_1 \end{bmatrix}\), \(f_2 = \begin{bmatrix} -x_2 \\ 0 \end{bmatrix}\), \(f_3 = \begin{bmatrix} 0 \\ x_3 \end{bmatrix}\), \(f_4 = \begin{bmatrix} x_4 \\ 0 \end{bmatrix}\)，\(x_i \geq 0\)，不能pull。

Judge Ax=b Solvable

在上节中，我们将Static Equilibrium方程组简化为了\(Ax=b, x_i \geq 0\)，并通过对于任意b是否能找到一个解x来判断A描述的抓取状态是否现成一个Form Closure。

那么，我们是如何判断对于任意b是否有解x的呢？我们说：“A的列空间的原点应该被A的列向量围成的tetrahedron包住”。

但事实上，这个描述并不够正式，我们有更正式的描述：

考虑\(Ax=b, A \in \mathbb{R}^{m\times n}, b \in \mathbb{R}^m, x \in \mathbb{R}^n, x_i \geq 0\)，对于任意b，存在一个解x的充分必要条件是：在\(\mathbb{R}^m\)中存在一个以原点为中心的open ball，落在A的列向量所现成的convex hull的中心。

这里就有一个概念了，convex hull是什么？

(EX1 begin)

对于下图而言，有3个\(\vec{a_i}\)，convex hull是一个三角形：

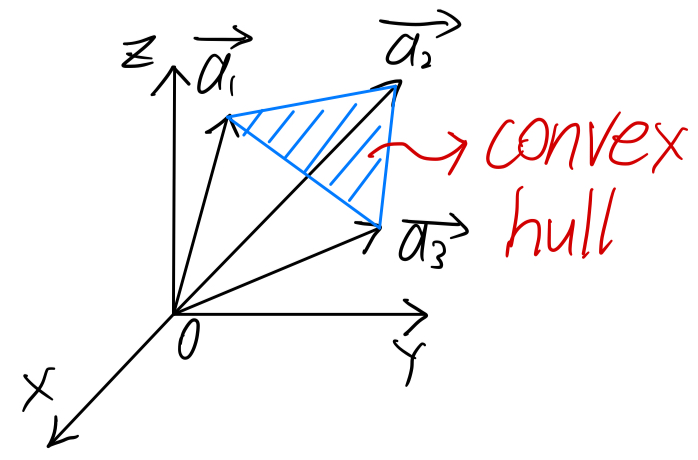
convex_hull_ex1

(EX1 end)

(EX2 begin)

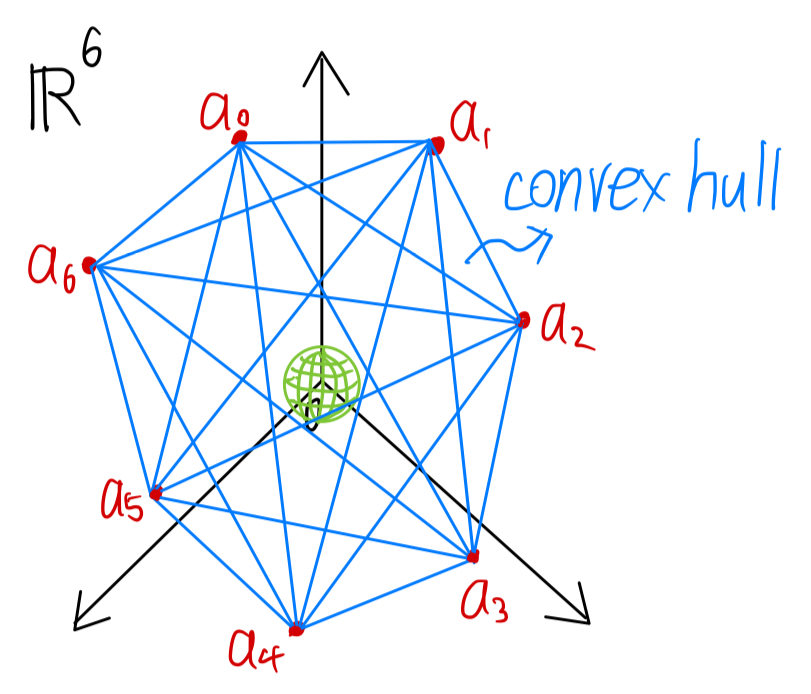
对于下图而言，有4个\(\vec{a_i}\)，convex hull是一个tetrahedron，你可以看到一个open ball落在A的列向量围成的convex hull里：

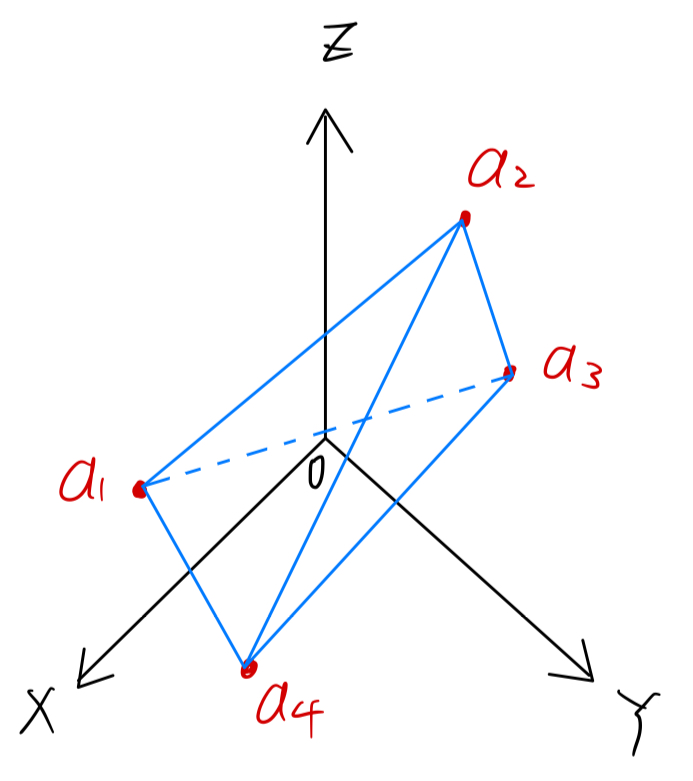
convex_hull_ex2

(EX2 end)

同样我们根据上例可以总结出两点：

对于平面抓取而言，若假设没有摩擦力，则至少4个frictionless point contact是必须的，如EX2。不然，要是只有3个contact point，则会变成EX1，不可能有open ball存在convec hull中的。

我们这里可以再扩展一下，对于3D空间抓取而言，至少需要几个frictionless point contact？我们来列出它的Static Equilibrium方程组，看看一共有多少的等式(即A有多少Row就知道了)，如下例：

(EX3 begin)

convex_hull_ex3

\[ \sum_{i=1}^n \vec{f_i}+\vec{f_{ext}}=0\;\;\; (3 equas) \\ \sum_{i=1}^n (\vec{r_i} \times \vec{f_i}) + \vec{r_{ext}} \times \vec{f_{ext}}=0\;\;\; (3 equas) \]

所以，假如没有摩擦力的话，我们至少需要7个手指去抓取，去现成Form Closure。

convex_hull_ex3_vector_space

感谢摩擦力的存在！

(EX3 end)

Grasps with Friction

摩擦力那么厉害，那我们现在就来考虑存在friction的抓取吧，也就是开始考虑Force Closure吧！

让我们从下面这个例子开始：

(EX1 begin)

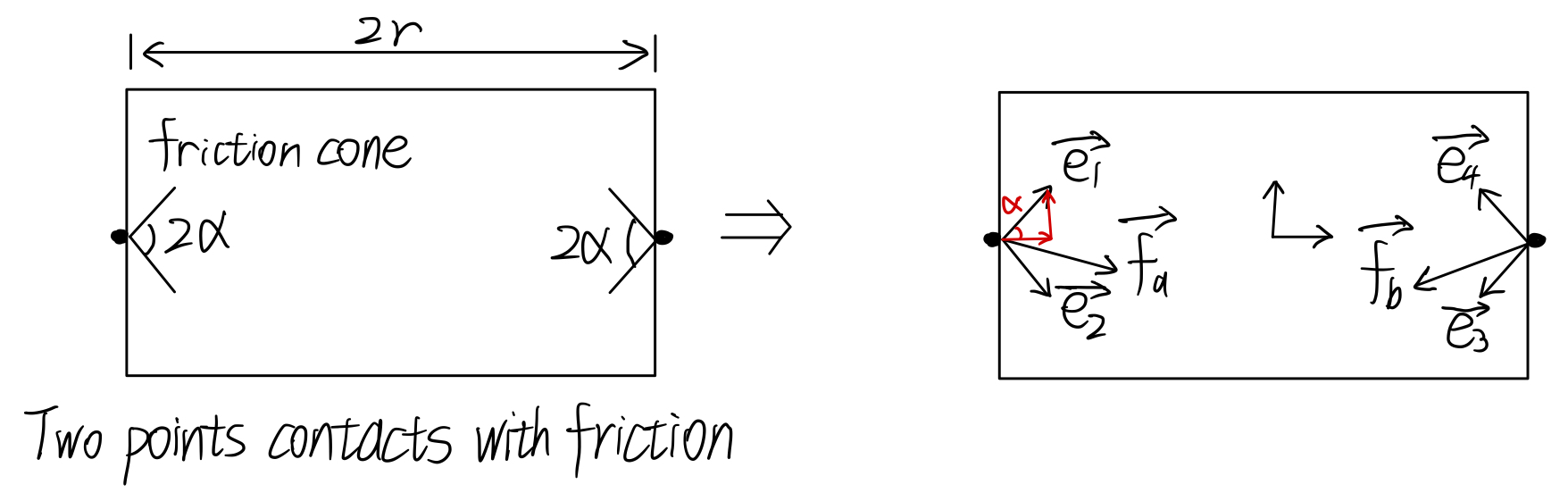
friction_grasp_ex1

记得，手指施加的力的方向必须在Friction Cone之中，否则会发生滑动。

上图可得： \[ \vec{f_a}=x_1 \vec{e_1} + x_2 \vec{e_2} \\ \vec{f_a}=x_3 \vec{e_3} + x_4 \vec{e_4} \\ \vec{e_1}=\begin{bmatrix} 1 \\ \eta \end{bmatrix}, \vec{e_2}=\begin{bmatrix} 1 \\ -\eta \end{bmatrix}, \vec{e_3}=\begin{bmatrix} -1 \\ -\eta \end{bmatrix}, \vec{e_4}=\begin{bmatrix} -1 \\ \eta \end{bmatrix} \\ x_i \geq 0,\;\;\; you\;\; can\;\; only\;\; push \]

可得Static Equilibrium方程组： \[ \vec{f_a}+\vec{f_b}+\vec{f_ext}=0 \\ m_a + m_b + m_{ext}=0 \] 即： \[ \begin{bmatrix} 1 & 1 & -1 & -1 \\ \eta & -\eta & -\eta & \eta \\ -r \eta & r \eta & -r \eta & r \eta \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} -f_{ext,x} \\ -f_{ext,y} \\ -m_{ext,z} \end{bmatrix} \]

那么，这里能否现成一个Force Closure呢？

也就是说，对于任意b而言，是否都存在一个x可行解呢？你画一下A的列向量围成的convex hull就知道了。这里是Force Closure。

(EX1 end)

其实，在现实中，friction就是存在的，而且我们考虑的一般都是Force Closure，那每次分析一个样例是否形成Force Closure都要去列Ax=b，然后画A的列空间，太麻烦了。

我们有一个更简单的方法来判断某个抓取是否形成Force Closure，即阮定理(Nguyen’s Theorem)：

对于一个平面抓取而言，若抓取点只有两个，且是带有摩擦力的，则现成Force Closure的充分必要条件是：连接两个接触点的直线都在Friction Cone中。如下图：

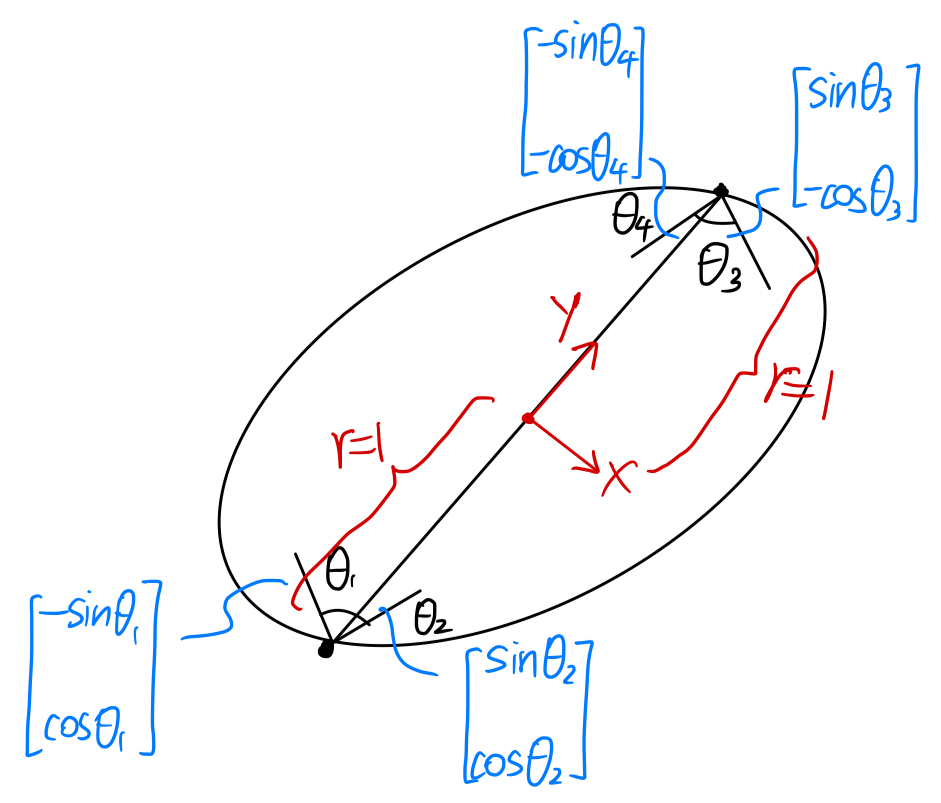
nguyen_theorem_postive

上图能形成Force Closure，下图则是形成不了Force Closure的负样例：

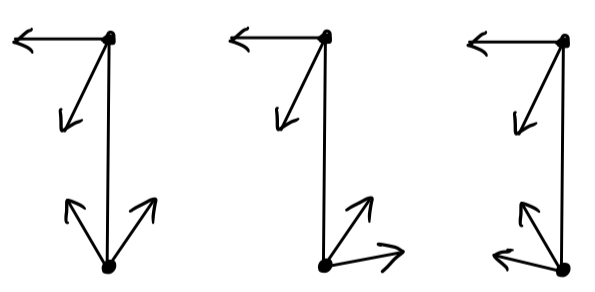
nguyen_theorem_negative

如何证明Nguyen’s Theorem？你可以列出它的Static Equilibrium方程组，对着上面的4个样例一个一个画A矩阵列空间验证一下： \[ \begin{bmatrix} -sin\theta_1 & sin\theta_2 & sin\theta_3 & -\theta_4 \\ cos\theta_1 & cos\theta_2 & -cos\theta_3 & -cos\theta_4 \\ -sin\theta_1 & sin\theta_2 & -sin\theta_3 & -sin\theta_4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} -f_{ext,x} \\ -f_{ext,y} \\ -m_{ext,z} \end{bmatrix} \]